向量及其运算

平面与向量

平面与点

平面(plane)是一种二维空间，可以将其比作一张纸。点(point)是位置的参照，可以使用一个二维的点表示平面中的一个位置。在这个二维空间中可能分布着许多点，为了描述一个点，需要两个信息，如水平位置和竖直位置。原点(origin)是一个参考点，用于描述其它点在平面中的相对位置。

为了测量平面内一个点的位置，需要两把尺子，这两把尺子称为坐标轴(axes, the singular is axis)，它们相交于原点，且彼此垂直。水平的轴称为 \\( x \\) 轴，竖直的轴称为 \\( y \\) 轴。

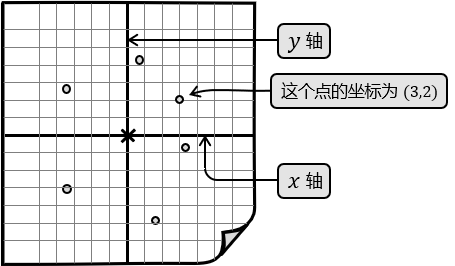
借助坐标轴，可以使用 \\( x \\) 坐标和 \\( y \\) 坐标定位具体的点。一般将二维坐标写成 \\( x \\) 坐标和 \\( y \\) 坐标的有序数对（数组）\\( (x,y) \\) ，例如 \\( (5,3) \\) 。

向量的基本概念

向量(vector)是具有方向和大小的量，可以用一个箭头表示向量：箭头的长度表示向量的大小，箭头的指向表示向量的方向：

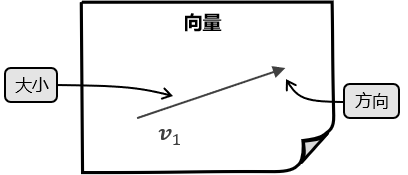
向量的特征只由它的大小与方向决定，而与它在什么位置无关。因此，经任意平移得到的依然是同一个向量：

在二维平面中，可以使用两个点表示一个向量，两点的方向确定向量的方向，两点的距离确定向量的大小。由于平移不改变向量，因此往往使用原点作为向量的起点（箭头的尾部）。因此，在平面中，向量可以理解成从原点指向一个具体的点的一个直线箭头，也可以理解为平面上（相对于原点的）任意一个点，可以使用点的方式表示向量，也可以使用点的坐标描述向量。

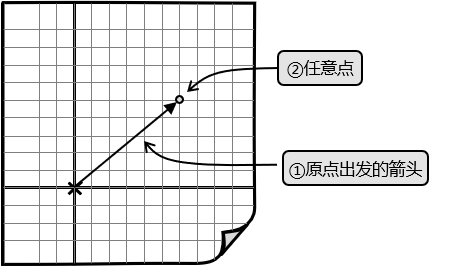
为了区别于点，一般将向量记为加粗的符号，例如 \\( \Vec v \\) 。

向量是一种解决问题的实用工具。在现实世界中许多物理量都具有大小和方向，此时它们就可以通过向量表示；在解析几何中，向量是计算几何体间的相对位置的实用工具。除此之外，向量也可以用作描述若干数构成的有序数组。

向量和普通的数一样，可以参与各种运算。接下来简单介绍平面向量的一些简单运算。

平面向量运算

向量加法

将两个数相加就是将它们合并在一起。同样，向量加法等价于将两个向量首尾相连，指向的新的向量：

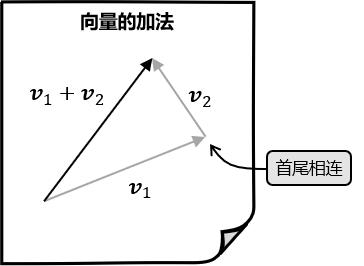
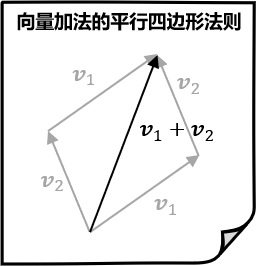
向量的加法和实数加法一样满足交换律，这条定律有时也称为向量加法的平行四边形法则，因为两种相加的顺序构成了一个平行四边形，指向同一个位置：

向量的标量乘法

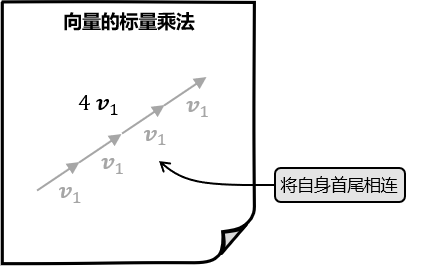
将一个数与一个整数相乘，实际上就是将这个数自身重复相加若干次数。类似地，将向量与一个数相乘可以看作向量的重复相加这么多次，只要把箭头复制若干份，不断地首尾相连即可得出结果：

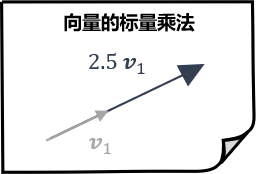
将向量乘以数的运算称为标量乘法(scalar multiplication)，普通的数通常被称为标量(scalar)。它的英文很形象，因为运算的效果就是将目标向量按给定的系数缩放(scale)。因此与向量相乘的标量也可以是小数。下图展示了这种运算，并将结果的箭头也按比例放大了：

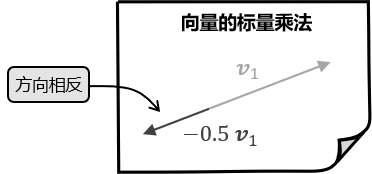
标量乘法还可以使用负数，使用负数代表沿相反方向缩放。例如，向量 \\( \Vec v \\) 与 \\( −0.5 \\) 的乘积，结果向量的长度是原向量的一半，而且指向相反的方向。

向量的分量和长度

直角坐标系下，一般将平行于坐标轴、长度为 1 的向量称为单位向量 ，分别记作 \\( \Vec e_x \\) 和 \\( \Vec e_y \\) 。根据向量的加法和数乘，任何一个向量都可以被分解为由单位向量经缩放和相加运算得到的结果：

因此，向量的坐标更严谨的表示方法是看作是组成它的单位向量前系数的有序组合。反之，给定一对有序数 \\( (x,y) \\) ，它既唯一确定了平面上的一个点，也唯一确定了由同一组单位向量组成的一个向量，这种情况下点和向量可以一一对应，因此可以使用点表示向量。

\\( v_x \Vec e_x \\) 和 \\( v_y \Vec e_y \\) 这两个沿坐标轴上的向量有时也被称为向量的分量，\\( (v_x,v_y) \\) 有时也称为向量的坐标 ，它和点的坐标一样都可以用于确定唯一的向量。向量的运算也可以看作是对各个坐标的运算：

相加得到的向量，其分量为被加的两个向量的分量之和。例如，向量 \\( \Vec u_1 = (3,4) \\) 和 \\( \Vec u_2 = (2,-1) \\) 相加，实际就是 \\( (3 \Vec e_x + 4 \Vec e_y) + (2 \Vec e_x + (-1) \Vec e_y) = (5 \Vec e_x + 3 \Vec e_y) \\) ，或者可以直接写成 \\( (3+2,4-1) = (5,3) \\) 的坐标相加形式。

向量 \\( \Vec v_1 = (4,3) \\) 与数 \\( 2.5 \\) 的乘积 \\( 2.5 \Vec v_1 \\) 等价于两个坐标各乘以 \\( 2.5 \\) ，结果为 \\( (10,7.5) \\) ，而且指向相同的方向。

因为两个坐标轴是垂直的，所以知道了向量的分量或坐标，就可以使用勾股定理计算向量的长度了。如果一个向量的坐标为 \\( (x,y) \\) ，那么它的长度为：

向量减法

有了向量加法，自然就有向量减法。对向量减法有两种理解方式：

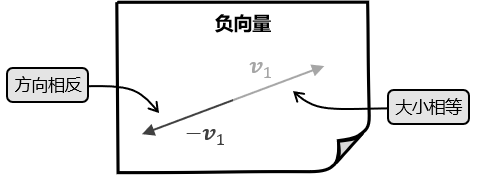
首先，一个数的负数等价于将这个数乘以 \\( −1 \\) ；同样，一个向量 \\( \Vec v \\) 的负向量 \\( −v \\) 也等价于将这个向量乘以 \\( −1 \\) ，即标量乘积 \\( -1\cdot \Vec v \\) ，结果长度相等，方向相反。如果 \\( \Vec v \\) 是 \\( (4,3) \\) ，那么它的负值 \\( −v \\) 等价于将两个分量乘以 −1（改变每个坐标值的符号），结果为 \\( (−4,−3) \\) 。

那么，向量减法 \\( \Vec v_1 - \Vec v_2 \\) 就等价于 \\( \Vec v_1 \\) 加上向量负值 \\( -\Vec v_2 \\) ，结果仍然遵守向量的缩放和加法三角形运算法则：

两个数的减法得到的是它们大小的差值，可以看作它们在数轴上对应两点的距离：

类似地，另一种理解向量相减的方式是，向量减法 \\( \Vec v_1 - \Vec v_2\\) 可以看作向量 \\( \Vec v_1 \\) 相对于向量 \\( \Vec v_2 \\) 的位置，也可以理解为从 \\( \Vec v_2 \\) 头部到 \\( \Vec v_1 \\) 头部的箭头：

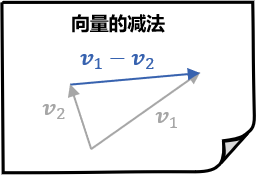
不管采用哪种理解方式，相减得到的向量坐标，同样为两个向量的坐标相减结果。例如，向量 \\( (5,4) \\) 和 \\( (3,1) \\) 相减的结果就是对应坐标相减的结果，为 \\( (2,3) \\) 。

从二维平面到三维空间

三维空间中的向量

在二维平面上，需要使用两个坐标来描述一个点的信息。二维向量有三种等价的表达：具有确定长度和方向的箭头、相对于原点的点，或者点对于的坐标 \\( (x,y) \\)。

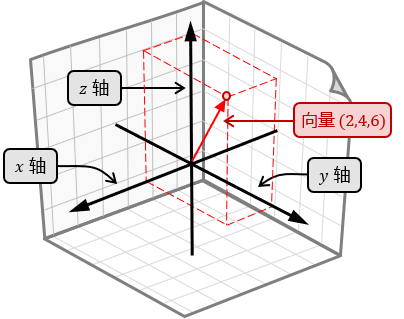
三维空间与二维平面类似，只是除了 \\( x \\) 方向和 \\( y \\) 方向外，还增加了 \\( z \\) 方向表示高度信息。三维向量也可以用类似的方式解释，只不过这个点在三维空间中，并且坐标需要使用三个数 \\( (x,y,z) \\) 描述：

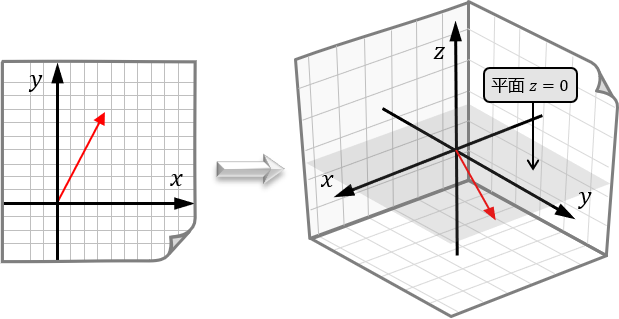
可以说，所有二维向量也都存在于三维空间中，只是位于高度 \\( z \\) 为零的平面上。

三维空间中的向量运算

在三维空间中向量的运算规律和二维向量非常类似。例如，向量加法也可以通过首尾相连向量，或将坐标分量相加来完成：

任意数量的三维向量相加，规律也和二维向量一样，可以将它们的所有 \\( x \\) 、\\( y \\) 和 \\( z \\) 坐标分别相加。

将三维向量乘以标量同样可以视为缩放，将其所有分量乘以标量系数便可以得到结果：

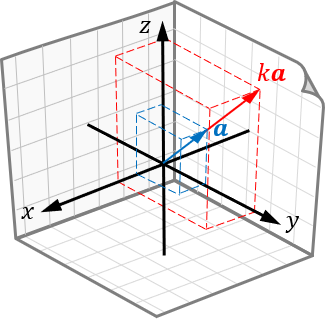
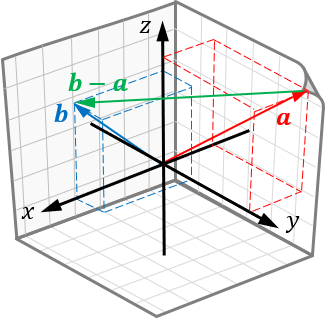
一个三维向量减去另一个三维向量，可以理解为从另一个向量头部到它头部的相对位置：

二维向量的距离可以使用勾股定理计算，而三维向量也可以使用勾股定理，只是需要构造一个辅助三角形：

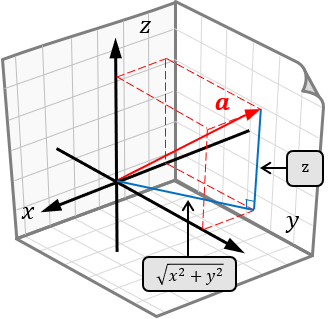
一个三维向量可以看成 \\( xy \\) 平面内的分量和 \\( z \\) 轴上的分量之和，\\( xy \\) 平面的分量长度计算可以通过勾股定理，类似二维向量；而这部分分量和 \\( z \\) 轴上的分量也构成了一个直角三角形，因此可以使用两次勾股定理计算三维向量的长度：

向量乘法

前面介绍了向量的加法、减法和标量乘法。但与实数不同的是，向量不满足四则运算，向量间的除法是没有意义的。不过向量之间可以相乘，具体来说，有两种相乘方式，它们的含义各不一样，分别代表了某种特定场景下的几何意义。

点积：测量向量对齐

点积(dot product)也叫内积(inner product)，是两个向量之间的运算。两个向量 \\( \Vec u \\) 和 \\( \Vec v \\) 的点积记作 \\( \Vec u \cdot \Vec v \\) 。点积适用于任意维度的向量，它返回一个标量（数），这个数可以被看作两个输入向量的对齐程度。

点积同时受到两个向量夹角和各自的长度影响，这是由于夹角相同的一对向量，如果它们更长，那么看起来相对更不对齐一些：

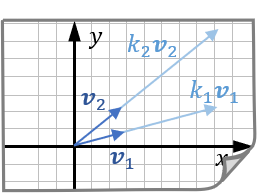
当向量夹角从 \\( 0 \\) 变到 \\( \dfrac \pi 2 \\) 时，点积 \\( \Vec u \cdot \Vec v \\) 从 \\( \Vec u \\) 和 \\( \Vec v \\) 长度乘积变到长度乘积的负值，这和余弦函数的变化规律相同，因此点积的计算公式为：

其中 \\( \theta \\) 是向量 \\( \Vec u \\) 和 \\( \Vec v \\) 之间的角度。

向量的点积也满足交换律，相乘的顺序不影响结果。并且和实数运算律一样，向量乘法的优先级高于向量加法，

首先以二维向量为例了解它们的点积。假设向量 \\( \Vec v_1 \\) 和 \\( \Vec v_2 \\) 的长度分别为 4 和 5 。如果它们的方向几乎相同，那么它们的点积为正，且大小近似等于它们长度之积，这意味着它们是基本对齐的：

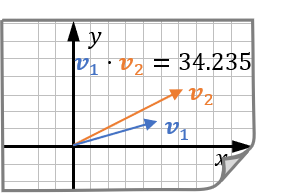
如果两个向量指向大致相反的方向，则其点积为负，且大致等于它们长度乘积的负数，这时可以说它们是反向对齐的：

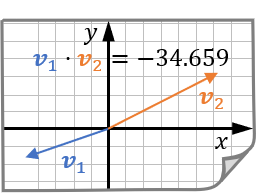
如果两个向量既不相同，也不相反，指向很不对齐，则其点积是一个远小于它们长度之积的数，正负主要看它们的指向是偏向相同还是偏向相反：

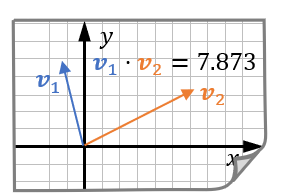
特别地，如果两个向量的方向完全垂直，那么无论它们的长度如何，点积都是零：

这种对齐程度还可以用向量的投影来衡量。如下图所示，想象在一束垂直向量 \\( \Vec u \\) 的灯光照射下，\\( \Vec v \\) 落在 \\( \Vec u \\) 方向上的可见部分就是 \\( \Vec v \\) 在 \\( \Vec u \\) 上的投影：

向量的点积反应了经投影后，投影方向上两个向量长度之积。显然，如果两个向量“靠的较近”，那么投影就较大，因此点积也较大。如果向量之间“离得较远”，投影便很小，使得点积也较小。

向量的点积还满足分配率，即：

接下来考虑点积的坐标计算式。如果根据坐标的定义展开点积，可以得到：

仔细观察拆分的这四项，\\( (u_x \Vec e_x) \cdot (u_x \Vec e_x) \\) 和 \\( (v_y \Vec e_y) \cdot (v_y \Vec e_y) \\) 都是向量与自身相乘，它们一定是对齐的，所以结果就等于它们的长度乘积；\\( (u_x \Vec e_x) \cdot (v_y \Vec e_y) \\) 和 \\( (u_y \Vec e_y) \cdot (v_x \Vec e_x) \\) 是两个垂直的向量相乘，它们完全不对齐，所以结果为 0 。因此可以得到计算点积的坐标运算公式：

也就是说，给定两个向量的坐标，其点积就是将相应的坐标相乘，然后将乘积相加。

可以通过坐标计算两个向量的长度和它们之间的角度得到点积的结果；反过来也可以通过坐标计算两个向量的长度和点积得到它们之间的角度。对上式变形，结果为：

这就是点积最重要的应用之一：点积可以在不做任何三角运算的情况下，判断两个向量或直线的相对方向。如果两个向量的点积为正，则向量的夹角小于 \\( 90^\circ \\) ；如果点积为负，则夹角大于 \\( 90^\circ \\) ；如果点积为 0 ，则两个向量垂直。这在三维空间很有用，因为在三维空间中，只需要确定坐标就可以计算向量长度和点积，但两个直线可能不在同一平面上，无法直接测量它们的夹角。

叉积：测量有向面积

和点积类似，叉积(cross product)也是向量之间的乘法运算。叉积也称外积(outer product)，两个向量 \\( \Vec u \\) 和 \\( \Vec v \\) 的叉积记作 \\( \Vec u \times \Vec v \\) 。

和点积不同的是，叉积只适合三维空间中的向量运算。叉积得到的结果是一个向量，它的大小代表两个向量确定的平行四边形的面积，方向代表两个向量在三维空间的方向。因此，点积有时也称数量积，叉积有时也称向量积。

叉积的长度也可视为两个向量的垂直程度，这和点积的定义非常相似，其计算公式为：

这个数值也可以视为由 \\( \Vec u \\) 和 \\( \Vec v \\) 围成的平行四边形的面积：

在介绍叉积的方向前，需要了解空间中的旋向。下图展示了两个合理的三维坐标系，并且使用同一套坐标生成了一对茶杯：

这两个茶杯看起来很像，但并不是完全一致的：它们呈镜像对称，如果将杯身的图案正对屏幕，那么杯柄将一个向左，一个向右。就像手套有左右手之分一样，不同的坐标系会引起三维空间方向上的歧义。

为了解决这个问题，需要有一个唯一的规则来确定坐标系的定义或坐标的空间朝向。这种规则称为右手法则(right-hand rule)，具体来说，如果使用右手的四指从 \\( x \\) 轴弯向 \\( y \\) 轴，那么拇指所指的方向规定为 \\( z \\) 轴的正向：

叉积的方向就是由 \\( \Vec u \\) 和 \\( \Vec v \\) 根据右手法则确定的朝向，从而叉积可以用作指明空间中的方向。

注意，叉积的运算是有顺序的，叉积运算并不满足交换律，具体来说：

叉积结果同时垂直于参与运算的两个向量，如果这两个向量确定了一个平面，那么叉积最重要的用途就是求解法向量。

因此，叉积运算实际上就是确定了这样一个向量：

叉积的另一个性质就是任意向量与自身的叉积都是零向量：

此外，叉积运算也满足分配律：

根据以上性质，可以推导叉积的坐标运算法则：

注意三维空间中一般规定 \\( \Vec e_x \times \Vec e_y = \Vec e_z \\) ，并且有 \\( \Vec e_y \times \Vec e_z = \Vec e_x, \\) \\( \Vec e_x \times \Vec e_z = - \Vec e_y, \\) \\( \Vec e_y \times \Vec e_y = \Vec 0 \\) 等，那么就可以得到：

向量积的运算比较复杂。如果了解行列式，那么倒是可以用行列式表达出来：