积分表(上)

\\[ \begin{align} (1). \cques{\int \frac{\dd x}{ax+b}} &= \frac 1 a \int \frac{\dd (ax)}{ax+b} = \frac 1 a \int \frac{\dd (ax+b)}{ax+b} \\ &= \cansw{\frac 1 a \ln |ax+b| + C} \end{align} \\]

\\[ \begin{align} (2). \cques{\int (ax+b)^\mu \dd x} &= \frac 1 a \int (ax+b)^\mu \dd (ax+b) = \frac 1 a \cdot \frac 1 {\mu+1} \int (\mu+1) (ax+b)^\mu \dd (ax+b) \\ &= \cansw{\frac 1 {a(\mu+1)} (ax+b)^{\mu+1} \qquad (\mu \neq -1)} \end{align} \\]

\\[ \begin{align} (3). \cques{\int \frac{x}{ax+b} \dd x} &= \frac 1 a \int \frac {ax+b-b}{ax+b} \dd x = \frac 1 a \int \left(1 - \frac b{ax+b}\right) \dd x\\ &= \frac 1 a \int \dd x - \frac 1 a \int \frac b {ax+b} \dd x = \cansw{\frac x a - \frac b {a^2} \ln |ax+b| + C} \end{align} \\]

\\[ \begin{align} (4). \cques{\int \frac {x^2}{ax+b} \dd x} &= \int \bigg( \frac x a - \frac b {a^2} + \cfrac{\cfrac{b^2}{a^2}}{ax+b} \bigg) \dd x = \frac 1 a \int x \dd x - \frac b {a^2} \int \dd x + \frac {b^2} {a^2} \int \frac{\dd x}{ax+b} \\ &= \cansw{\frac {1}{2a} x^2 - \frac b {a^2} x + \frac {b^2} {a^3} \ln|ax+b|+C} \end{align} \\]

\\[ \begin{align} (5). \cques{\int \frac{\dd x}{x(ax+b)}} &= \int \bigg(\frac{A_1}{x} + \frac{A_2}{ax+b}\bigg) \dd x = \int \bigg(\frac{\cfrac{1}{b_1}}{x} + \frac{-\cfrac a b}{ax+b}\bigg) \dd x \\ &= \frac 1 b \int \frac 1 x \dd x - \frac a b \int \frac{1}{ax+b} \dd x = \frac 1 b \ln |x| - \frac 1 b \ln|ax+b| +C \\ &= \cansw{\frac 1 b \ln|\frac{x}{ax+b}| + C} \end{align} \\]

\\[ \begin{align} (6). \cques{\int \frac{\dd x}{x^2(ax+b)}} &= \int \bigg(\frac{A_1} x + \frac{A_2}{x^2} + \frac{A_3}{ax+b}\bigg) \dd x = \int \bigg(\frac{-\cfrac{a}{b^2}}{x} + \frac{\cfrac{1}{b}}{x^2} + \frac{\cfrac{a^2}{b^2}}{ax+b} \bigg) \dd x \\ &= - \frac{a}{b^2}\int \frac{1}{x} \dd x + \frac 1 b \int \frac{1}{x^2} \dd x + \frac {a^2}{b^2} \int \frac 1 {ax+b} \dd x \\ &= -\frac a {b^2} \ln |x| - \frac 1 b \cdot \frac 1 x + \frac a {b^2} \ln |ax+b| + C \\ &= \cansw{\frac a {b^2} \ln \bigg|\frac{ax+b}{x}\bigg|-\frac 1 {bx} + C} \end{align} \\]

\\[ \begin{align} (7). {\cques{ \int \frac{x}{(ax+b)^2} \dd x }} = \int \bigg(\frac {A_1}{ax+b} + \frac {A_2}{(ax+b)^2}\bigg)\dd x = \int \bigg(\frac {\cfrac 1 a}{ax+b} + \frac {-\cfrac b a}{(ax+b)^2}\bigg)\dd x\\ = \frac 1 a \int \frac{\dd x}{ax+b} - \frac b a \int \frac{\dd x}{(ax+b)^2} = \cansw{\frac 1 {a^2} \ln |ax+b|+\frac {b} {a^2(ax+b)} + C} \end{align} \\]

\\[ \begin{align} (8). \cques{\int \frac{x^2}{(ax+b)^2} \dd x} &= \int \bigg(\frac 1 {a^2} + \frac{-\cfrac{2b} a x - \cfrac{a^2}{b^2}}{(ax+b)^2}\bigg) \dd x = \int \bigg(\frac 1 {a^2} + \frac{A_1}{ax+b} + \frac{A_2}{(ax+b)^2}\bigg) \dd x \\ &= \int \bigg(\frac 1 {a^2} + \frac{-\cfrac{2b}{a^2}}{ax+b} + \frac{\cfrac{b^2}{a^2}}{(ax+b)^2}\bigg) \dd x = \cansw{\frac 1 {a^2} x - \frac{2b}{a^3} \ln |ax+b|-\frac {b^2} {a^3} \cdot \frac 1 {ax+b}} \end{align} \\]

\\[ \begin{align} (9). \cques{\int \frac{\dd x}{x(ax+b)^2}}&=\int \bigg(\frac{A_1}x + \frac{A_2}{ax+b} + \frac{A_3}{(ax+b)^2}\bigg)\dd x =\int \bigg(\frac{\cfrac 1 {b^2}}x + \frac{-\cfrac a {b^2}}{ax+b} + \frac{-\cfrac a b}{(ax+b)^2}\bigg)\dd x\\ &= \frac 1 {b^2} \ln |x| - \frac 1 {b^2} \ln|ax+b| - \frac 1 b \cdot \frac 1 {ax+b} + C\\ &= \cansw{\frac 1 {b^2} \ln \bigg|\frac x {ax+b}\bigg| - \frac 1 {b(ax+b)} + C\\} \end{align} \\]

\\[ \begin{align} (10). \cques{\int \quB\dd x} &= \frac 1 a \int (ax+b)^\frac 1 2 \dd (ax) = \frac {2}{3a}\int \frac 3 2 (ax+b)^\frac 1 2 \dd (ax+b)\\ &= \cansw{\frac {2}{3a}(ax+b)^\frac 3 2 + C} \end{align} \\]

\\[ \begin{align} (11). \cques{\int x \quB \dd x} &= \frac 1 a \int (ax+b-b) (ax+b)^{\frac 1 2} \dd x = \frac 1 a \int (ax+b)^{\frac 3 2} \dd x - \frac b a \int (ax+b)^{\frac 1 2} \dd x \\ &= \frac 2 {5a^2} (ax+b)^{\frac 5 2} - \frac{2b}{3a^2}(ax+b)^{\frac 3 2} + C = \cansw{\frac 2{15a^2}(3ax-2b)(ax+b)^{\frac 3 2} + C} \end{align} \\]

\\[ \begin{align} (12). \cques{\int x^2 \quB \dd x} &= \frac 1 {a^2} \int [(ax+b)^2-2abx-b^2] \quB \dd x\\ &= \frac 1 {a^2} \int (ax+b)^{\frac 5 2} \dd x - \frac {2b} a \int x \quB \dd x - \frac {b^2}{a^2} \int \quB \dd x \\ &= \frac 2 {7a^3}(ax+b)^{\frac 7 2} - \frac {2b}{a} \left[ \frac 2{15a^2}(3ax-2b)(ax+b)^{\frac 3 2} \right] - \frac {2b^2}{3a^3}(ax+b)^\frac 3 2\\ &= \cansw{\frac 2 {15a^3} (3a^2x^2-4abx+8b^2)(ax+b)^{\frac 3 2} + C} \end{align} \\]

\\[ \begin{align} (13). \cques{\int \fc x {\quB} \dd x} &= \fc 1 a \int \fc {\quA - b}{\sqrt{\quA}} \dd x = \fc 1 a \int (\quA)^{\fc 1 2} \dd x - \fc b a \int (\quA)^{-\fc 1 2} \dd x\\ &= \cansw{\fc 2 {3a^2}(ax-2b)\quB + C} \end{align} \\]

\\[ \begin{align} (14). \cques{\int \fc {x^2}{\quB} \dd x} &= \fc 1 {a^2} \int \fc {(\quA)^2-2abx-b^2}{\quB} \dd x \\ &= \fc 1 {a^2} \int (\quA)^{\fc 3 2} - \fc {2b} a \int \fc x {\quB} \dd x - \fc {b^2}{a^3} \int \fc 1 {\quB} \dd x\\ &= \fc 2 {5a^3}(\quA)^\fc 5 2 - \fc {2b} a \left[ \fc 2 {3a^2}(ax-2b)\quB \right] - \fc {2b^2}{a^3} (\quA)^\fc 1 2 + C \\ &= \cansw{\fc 2 {15a^3}(3a^2x^2-4abx+8b^2)\quB + C} \end{align} \\]

\\[ \begin{align} (15). \cques{\int \fc {\dd x }{x \quB}} &\xlongequal{\textstyle u=\quB} \int \cfc {\cfc 1 a 2u \dd u}{\cfc{u^2-b} a u} = 2 \int \fc {\dd u}{u^2-b} \\ &= \begin{cases} (b > 0) &\displaystyle \int \fc 1 {\sq{b}} \left( { \fc 1 {u-\sq{b}} - \fc 1 {u+\sq{b}} } \right) \dd u = \fc 1 {\sq{b}} \ln \left| {\fc {u-\sq{b}}{u+\sq{b}}} \right| + C \\ (b < 0) &\displaystyle 2 \int \fc 1 {1 + (\cfc {u}{\sq{-b}} )^2} \dd u = \fc 2 {\sq{-b}} \arctan \left(\cfc {u}{\sq{-b}} \right) + C \end{cases} \\ &= \cansw{ \begin{cases} (b > 0) &\displaystyle \fc 1 {\sq{b}} \ln \left| {\fc {\quB-\sq{b}}{\quB+\sq{b}}} \right| + C\\ (b < 0) &\displaystyle \fc 2 {\sq{-b}} \arctan \sq{\cfc {\quA}{-b}} + C \end{cases} } \\ \end{align} \\]

\\[ \begin{align} (18). \cques{\int \fc {\quB} {x^2} \dd x} &= \int \quB \dd \abig(){-\frac 1 x} = -\fc 1 x \quB - \int - \fc 1 x \dd (\quB) \\ &= \cansw{-\fc{\quB}{x} + \fc a 2 \int \fc{\dd x}{x \quB} = \dots} \end{align} \\]

\\[ \begin{align} (17). \cques{\int \fc {\quB}{x} \dd x} &\xlongequal{\textstyle u=\quB} \int \fc {au}{u^2-b} \cdot \fc 1 a 2u \dd u = \int \fc{2u^2}{u^2-b} \dd u\\ &= \int \abig(){2+\fc{2b}{u^2-b}} \dd u = 2u + b \int \fc{2\dd u}{u^2-b} \\ &= \cansw{2 \quB + b \int \fc{\dd x}{x \quB} = \dots} \end{align} \\]

\\[ \begin{align} (16). \cques{\int \fc{\dd x}{x^2 \quB}} &= \int \bigg( \fc {A_1 \quB}{x^2} + \fc {A_2}{x \quB} \bigg)\dd x = \int \bigg( \fc {\cfc 1 b \quB}{x^2} + \fc {-\cfc a b}{x \quB} \bigg)\dd x \\ &= \cansw{\fc 1 b\int \fc {\quB} {x^2} \dd x - \fc a b \int \fc{\dd x}{x \quB} = -\fc{\quB}{bx} - \fc a {2b} \int \fc{\dd x}{x \quB} = \dots} \end{align} \\]

\\[ \begin{align} (19). \cques{\int \fc {\dd x}{x^2+a^2}} &= \int \fc {\dd \cfc x a}{1+(\cfc x a)^2}\\ &= \cansw{\fc 1 a \arctan \fc x a + C} \end{align} \\]

\\[ \begin{align} (21). \cques{\int \fc {\dd x}{x^2-a^2}} &= \int \fc 1 {2a} \left( \fc 1 {x-a} - \fc 1 {x+a} \right) \dd x = \fc 1 {2a} \left( \int \fc {\dd (x-a)}{x-a} - \int \fc {\dd (x+a)}{x+a} \right) \\ &= \cansw{\fc 1 {2a} \ln \left| \fc{x-a}{x+a} \right| + C} \end{align} \\]

\\[ \begin{align} (20). \cques{\int \fc {\dd x}{(x^2+a^2)^n}} &= \fc x {(x^2+a^2)^n} - \int x \dd \abig[]{\fc 1 {(x^2+a^2)^n}} = \fc x {(x^2+a^2)^n} - \int x \cdot \fc {-n}{(x^2+a^2)^n} \cdot 2x \dd x \\ &= \fc x {(x^2+a^2)^n} + 2n \int \fc {x^2+a^2-a^2}{(x^2+a^2)^{n+1}} \dd x\\ &= \fc x {(x^2+a^2)^n} + 2n \int \fc 1 {(x^2+a^2)^n} \dd x - 2na^2 \int \fc 1 {(x^2+a^2)^{n+1}} \dd x \end{align} \\]

\\[ \quad \text{so, } \quad \cques{\int \fc {\dd x}{(x^2+a^2)^{n+1}}} = \cansw{\fc x {2na^2(x^2+a^2)^n} + \fc {2n-1}{2na^2} \int \fc {\dd x}{(x^2+a^2)^n} + C} \\]

\\[ \begin{align} (22). \cques{\int \fc {\dd x}{\quC}} &= \begin{cases} (b>0) & \displaystyle \int \fc {\dd x}{(\sq{a}x)^2 + (\sq{b})^2} \xlongequal[\textstyle d=\sq{b}]{\textstyle u=\sq a x} \fc 1 {\sq a} \int \fc {\dd u}{u^2 + d^2} \\ (b<0) & \displaystyle \int \fc {\dd x}{(\sq{a}x)^2 - (\sq{-b})^2} \xlongequal[\textstyle d=\sq{-b}]{\textstyle u=\sq a x} \fc 1 {\sq a} \int \fc {\dd u}{u^2 - d^2} \end{cases} \\ &= \begin{cases} (b>0) & \displaystyle \fc 1 {\sq a d} \arctan \fc u d + C = \cansw{\fc 1 {\sq {ab}} \arctan \sq{\fc a b} x + C} \\ \displaystyle (b<0) & \displaystyle \fc 1 {2\sq a d} \ln \abig||{\fc{u-d}{u+d}} + C = \cansw{\fc 1 {2\sq {-ab}} \ln \abig||{\fc{\sq a x - \sq{-b}}{\sq a x + \sq{-b}}} + C} \end{cases} \end{align} \\]

\\[ \begin{align} (23). \cques{\int \fc x {\quC}} \dd x &= \fc 1 2 \int \fc {\dd (x^2)}{\quC} \\ &= \fc 1 {2a} \int \fc {\dd (\quC)}{\quC} = \cansw{\fc 1 {2a} \ln |\quC| + C} \end{align} \\]

\\[ \begin{align} (24). \cques{\int \fc {x^2}{ax^2+b} \dd x} &= \fc 1 a \int \fc {ax^2+b-b}{ax^2+b} \dd x = \fc 1 a \int (1-\fc {b}{ax^2+b}) \dd x\\ &= \cansw{\fc x a - \fc b a \int \fc {\dd x}{\quC} + C = \dots} \end{align} \\]

\\[ \begin{align} (25). \cques{\int \fc {\dd x}{x(\quC)}} &= \int \abig(){\fc {A_1} x + \fc {A_2 x + A_3}{\quC}} \dd x = \int \bigg( {\fc {\cfc 1 b} x + \fc {-\cfc a b x}{\quC}} \dd x \bigg) \\ &= \cansw{\fc 1 b \ln |x| - \fc a b \int \fc x {\quC} \dd x + C = \fc 1 {2b} \ln \abig||{\fc {x^2}{\quC}} + C} \end{align} \\]

\\[ \begin{align} (26). \cques{\int \fc {\dd x}{x^2(\quC)}} &= \int \abig(){\fc {A_1} {x^2} + \fc {A_2}{\quC}} \dd x = \int \bigg( \fc {\cfc 1 b}{x^2} + \fc{-\cfc a b}{\quC} \bigg) \dd x \\ &= \cansw{-\fc 1 {bx} - \fc a b \int \fc {\dd x}{\quC} + C = \dots} \end{align} \\]

\\[ \begin{align} (27). \cques{\int} & \xlongequal{\textstyle x = \sq u} \int \fc {\cfc 1 {2 \sq u} \dd u}{u \sq u (au+b)} = \cansw{\fc 1 2 \int \fc {\dd u}{u^2(au+b)} + C} \\ &= \cansw{- \fc 1 {2bx^2} + \fc a {2b^2} \ln \abig||{\fc {ax^2+b}{x^2}} + C} \end{align} \\]

\\[ \begin{align} (28). \cques{\int \fc {\dd x}{(\quC)^2}} &= \fc 1 {2a} \int \fc {x \dd x}{x (\quC)^2} = \fc 1 {2a} \int \fc {\dd (\quC)}{x (\quC)^2} = - \fc 1 {2a} \int \fc 1 x \dd \abig(){\fc 1 \quC} \\ &= \cansw{- \fc 1 {2ax(\quC)} - \fc 1 {2a} \int \fc {\dd x}{x^2(\quC)} + C} \\ &= \cansw{\fc x {2b(\quC)} + \fc 1 {2b} \int \fc {\dd x}{\quC}} \end{align} \\]

\\[ \begin{align} (29). \cques{\int \fc {\dd x}{\quD}} &= \int \fc {\dd x} {a \abig(){x+\cfc b {2a}}^2 + \cfc {4ac-b^2}{4a}} \xlongequal[\textstyle d = \dfc {4ac-b^2}{4a}]{\textstyle u = x + \dfc b {2a}} \cansw{ \int \fc {\dd u}{au^2+d} } \\ &= \cansw{\begin{cases} (4ac-b^2>0) & \displaystyle \fc 2 {\sq {4ac-b^2}} \arctan \fc {2ax+b}{\sq {4ac-b^2}} + C \\ (4ac-b^2 < 0) & \displaystyle \fc 1 {\sq {b^2-4ac}} \ln \abig||{\fc {2ax+b-\sq{b^2-4ac}}{2ax+b+\sq{b^2-4ac}}} + C \end{cases}} \end{align} \\]

\\[ \begin{align} (30). \cques{\int \fc x {\quD} \dd x} &= \fc 1 2 \int \fc {\dd x^2} {\quD} = \fc 1 {2a} \int \fc {\dd (\quD)}{\quD} - \fc 1 {2a} \int \fc {\dd (bx+c)}{\quD} \\ &= \cansw{\fc 1 {2a} \ln |\quD| - \fc b {2a} \int \fc {\dd x}{\quD} + C} \end{align} \\]

\\[ \begin{align} (31). \cques{\int \fc {\dd x}{\quE}} & \xeqt{x=a\tan t} \int \fc {a \sec^2 t}{a\sec t} \dd t = \int \sec t \dd t = \ln |\sec t + \tan t| + C_1\\ &= \ln \abig||{\fc{\quE} a + \fc x a} + C_1 = \cansw{\ln |\quE+x| + C} \end{align} \\]

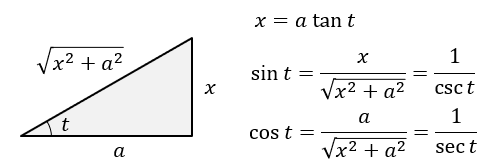
\\[ \begin{align} (32). \cques{\int \fc {\dd x}{(\quE)^3}} & \xeqt{x=a\tan t} \int \fc {a\sec^2 t \dd t}{a^3 \sec^3 t} = \fc 1 {a^2} \int \cos t \dd t\\ &= \fc {\sin t}{a^2} + C = \cansw{\fc x {a^2\quE} + C} \end{align} \\]

\\[ \begin{align} (33). \cques{\int \fc x {\quE} \dd x} &= \int \fc {\dd (x^2+a^2)}{2\quE} = \cansw{\quE + C} \end{align} \\]

\\[ \begin{align} (34). \cques{\int \fc x {(\quE)^3}} \dd x &= \int (x^2+a^2)^{-\fc 3 2} \cdot \fc 1 2 \dd (x^2+a^2) = \cansw{- (x^2+a^2)^{-\fc 1 2} + C} \end{align} \\]

\\[ \begin{align} (41). \cques{\int x \quE \dd x} &= \fc 1 2 \int (x^2+a^2)^{\fc 1 2} \dd (x^2+a^2) = \cansw{\fc 1 3 (x^2+a^2)^{\fc 3 2} + C} \end{align} \\]

\\[ \begin{align} \int \sec ^n x \dd x &= \int \sec ^{n-2} x \dd (\tan x) = \int \tan x \sec ^{n-2} x - \int \tan x \dd (\sec ^{n-2} x) \\ &= \tan x \sec ^{n-2} x - \int (n-2) \sec ^{n-2} x \tan^2 x \dd x \\ &= \tan x \sec ^{n-2} x - \int (n-2) \sec ^{n-2} x (\sec^2 x - 1) \dd x \\ &= \tan x \sec ^{n-2} x - (n-2) \int sec ^n x \dd x + (n-2) \int \sec ^{n-2} x \dd x \end{align} \\]

\\[ \int \sec^3 x \dd x = \fc 1 2 (\tan x \sec x + \ln |\sec x + \tan x|) + C \\]

\\[ \int \sec^5 x \dd x = \fc {\tan x \sec ^3 x} 4 + \fc 3 8 (\tan x \sec x + \ln|\sec x+ \tan x |)+C \\]

\\[ \begin{align} (35). \cques{\int \fc {x^2}{\quE} \dd x} & \xeqt{x=a\tan t} \int \fc {a^2\tan^2 t}{a\sec t} \cdot a \sec ^2 t \dd t = a^2 \int (\sec ^2 t - 1) \sec t \dd t \\ &= a^2 \int \sec ^3 t \dd t + a^2 \int \sec t \dd t = \fc {a^2} 2 \tan t \sec t - \fc {a^2} 2 \ln |\sec t + \tan t| + C_1 \\ &= \cansw{\fc 1 2 x \quE - \fc {a^2}2 \ln|x+\quE| + C} \end{align} \\]

\\[ \begin{align} (36). \cques{\int \fc {x^2}{(\quE)^3} \dd x} & \quEsub \int \fc {a^2\tan^2 t}{a^3\sec^3 t} a \sec^2 t \dd t \\ &= \int \fc {\sec^2 t - 1}{\sec t} \dd t = \int \sec t \dd t - \int \cos t \dd t \\ &= \cansw{\ln |x+\quE| - \fc x {\quE} + C} \end{align} \\]

\\[ \begin{align} (37). \cques{\int \fc {\dd x}{x \quE}} &\quEsub \int \fc 1 {a \tan t \cdot a \sec t} a \sec^2 t \dd t \\ &= \fc 1 a \int \csc t \dd t = \cansw{\fc 1 a \ln \abig||{\fc {\quE - a} x} + C} \end{align} \\]

\\[ \begin{align} (38). \cques{\int \fc {\dd x}{x^2 \quE}} & \quEsub \int \fc 1 {a^2 \tan^2 t} \cdot \fc 1 {a \sec t} \cdot a \sec^2 t \dd t\\ &= \fc 1 {a^2} \int \fc {\sec t }{\tan ^2 t} \dd t = \fc 1 {a^2} \int \fc {\cos t}{\sin^2 t}\dd t = \fc 1 a^2 \cdot -\fc 1 {\sin t} \\ &= \cansw{- \fc {\quE}{a^2x} + C} \end{align} \\]

\\[ \begin{align} (39). \cques{\int \sq {x^2+a^2} \dd x} & \quEsub \int a \sec t \cdot a \sec ^2 t \dd t = a^2 \int \sec ^3 t \dd t \\ &= \fc {a^2} 2 (\tan t \sec t + \ln |\sec t + \tan t|+C) \\ &= \cansw{\fc {x\quE} 2 + \fc {a^2} 2 \ln |x+\quE| + C} \end{align} \\]

\\[ \begin{align} (40). \cques{\int (\quE)^3 \dd x} & \quEsub \int a^3 \sec ^3 t \cdot a \sec^2 t \dd t = a^4 \int \sec ^5 t \dd t \\ &= a^4\bigg[\fc {x (x^2+a^2)^{\fc 3 2}}{4a^4} + \fc 3 8 \abig(){\fc {x\quE}{a^2} + \ln \abig||{\fc x a+\fc {\quE} a}}\bigg] + C_1 \\ &= a^4 \abig[]{\fc {\quE}{4a^4} x (x^2+a^2) + \fc 3 {2a} x \fc {\quE}{4a}+ \fc 3 8 \ln |x + \quE|} + C\\ &=\cansw{x\quE \fc {2x^2+5a^2} 8 + \fc 3 8 a^4 \ln |x+\quE| + C} \end{align} \\]

\\[ \begin{align} (42). \cques{\int x^2 \quE \dd x} & \quEsub \int a^2 \tan^2 t \cdot a \sec t \cdot a \sec^2 t \dd t = \int a^4 (\sec^2 t - 1) \sec^3 t \dd t\\ &= a^4 \int \sec^5 t \dd t - a^4 \int \sec ^3 t \dd t = \fc {a^4} 4 \tan t\sec ^3 t - \fc {a^4} 8 \tan t\sec t - \fc {a^4} 8 \ln |\sec t +\tan t| + C_1 \\ &= \cansw{\fc {x\quE} 8 (2x^2+a^2) - \fc {a^4} 8 \ln|x+\quE| + C} \end{align} \\]

\\[ \begin{align} (43). \cques{\int \fc {\quE}x \dd x } & \quEsub \int \fc {a\sec t}{a\tan t } \cdot a \sec ^2 \dd t = a \int \fc {\sec t}{\tan t} (1+\tan^2 t) \dd t \\ &= a\int \csc t \dd t + a \int \sec t \tan t \dd t = a \ln |\csc t - \cot t| + a \sec t + C_1\\ &= \cansw{a\ln \abig||{\fc {\quE - a} x} + \quE + C} \end{align} \\]

\\[ \begin{align} (44). \cques{\int \fc{\quE}{x^2} \dd x} & \quEsub \int \fc {a\sec t }{a^2 \tan^2 t } \cdot a \sec^2 \dd t = \int \fc {\sec t}{\tan^2 t}(1+\tan^2 t) \dd t\\ &= \int \fc {\cos t }{\sin^2 t} \dd t + \int \sec t \dd t = -\fc 1 {\sin t}+ \ln|\sec t +\tan t | + C_1 \\ &= \cansw{-\fc {\quE} x + \ln|x+\quE| + C} \end{align} \\]

\\[ \begin{align} (47). \cques{\int \fc x {\quF} \dd x} &= \int \fc {\dd (\quFF)}{2\quF} \dd x = \cansw{\quF + C} \end{align} \\]

\\[ \begin{align} (48). \cques{\int \fc x {(\quF)^3} \dd x} &= \int (\quFF)^{-\fc 3 2} \cdot \fc 1 2 \dd (\quFF) = \cansw{-(\quFF)^{\fc 1 2} + C} \end{align} \\]

\\[ \begin{align} (55). \cques{\int x \quF \dd x} &= \int (\quFF)^{\fc 1 2} \cdot \fc 1 2 \dd (\quFF) = \cansw{\fc 1 3 (\quFF)^{\fc 3 2} + C} \end{align} \\]

\\[ \begin{align} (45). \cques{\int \fc {\dd x}{\quF}} & \quFsub \int \fc {a\sec t \tan t \dd t}{a\tan t} = \int \sec t \dd t \\ &= \ln|\fc{\quF} a + \fc x a| + C_1 = \cansw{\ln|\quF + x| + C} \end{align} \\]

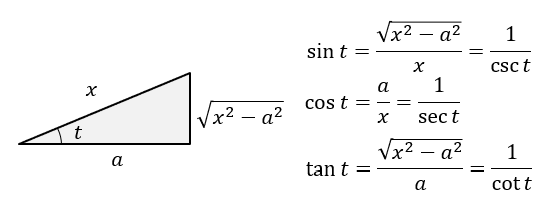
\\[ \begin{align} (46). \cques{\int \fc {\dd x}{(\quF)^3}} & \quFsub \int \fc{a\sec t \tan t \dd t}{a^3\tan^3 t} \\ &= \fc 1 {a^2} \int \fc {\cos t}{\sin^2 t} \dd t = - \fc 1 {a^2 \sin t} = \cansw{-\fc x {a^2 \quF} + C} \end{align} \\]

\\[ \begin{align} (49). \cques{\int \fc {x^2}{\quF} \dd x} & \quFsub \int \fc {a^2 \sec ^2 t}{a \tan t} \cdot a\sec t \tan t \dd t = a^2 \int \sec ^3 t \dd t \\ &= \fc {a^3} 2 (\tan t \sec t + \ln |\sec t + \tan t|) + C_1\\ &= \cansw{\fc 1 2 x\quF + \fc {a^2}2 \ln |\quF + x| + C} \end{align} \\]

\\[ \begin{align} (50). \cques{\int \fc {x^2}{(\quF)^3} \dd x} & \quFsub \int \fc {a^2 \sec^2 t}{(a\tan t)^3} a\sec t \tan t \dd t = \int \csc^2 t\sec t \dd t\\ &= \int \sec t \cdot -\dd (\cot t) = -\sec t \cot t + \int \cot t \dd (\sec t)\\ &= -\csc t + \int \sec t \dd t = \cansw{-\fc x {\quF} + \ln|x+\quF| + C} \end{align} \\]

\\[ \begin{align} (52). \cques{\int \fc {\dd x}{x^2 \quF}} & \quFsub \int \fc {a \sec t \tan t \dd t}{a^2 \sec^2 t \cdot a\tan t}\\ &= \fc 1 {a^2} \int \cos t \dd t = \fc {\sin t}{a^2} +C = \cansw{\fc {\quF}{a^2x} + C} \end{align} \\]

\\[ \begin{align} (53). \cques{\int \quF \dd x} & \quFsub \int a\tan t \cdot a \sec t \tan t \dd t = a^2 \int \sec t (\sec^2 t - 1) \dd t\\ &= a^2 \int \sec^3 t \dd t - a^2 \int \sec t \dd t = \fc {a^2} 2 (\tan t \sec t ) - \fc {a^2} 2 \ln |\sec t + \tan t | + C_1\\ &= \cansw{\fc {x\quF} 2 - \fc {a^2} 2 \ln |x + \quF| + C} \end{align} \\]

\\[ \begin{align} (54). \cques{\int (\quF)^3 \dd x} & \quFsub \int a^3 \int a^3 \tan^3 t \cdot a\sec t \tan t \dd t = a^4 \int (\sec^2 t - 1)^2 \sec t \dd t\\ &= a^4 \int \sec^5 t \dd t - 2 a^4 \int \sec^3 t \dd t + a^4 \int \sec t \dd t \\ &= \fc 1 4 a^4 \tan t \sec^3 t - \fc 5 8 a^4 \tan t\sec t + \fc 3 8 a^4 \ln|\sec t + \tan t| + C_1\\ &= \cansw{\fc 1 8 (2x^2-5a^2) x\quF + \fc 3 8 a^4 \ln|x+\quF| + C} \end{align} \\]

\\[ \begin{align} (56). \cques{\int x^2 \quF \dd x} & \quFsub \int a^2 \sec^2 t \cdot a \tan t \cdot a \sec t \tan t \dd t = a^4 \int \sec^3 t (\sec^2 t - 1) \dd t\\ &= a^4 \int \sec^5 t \dd t - a^4 \int \sec^3 t \dd t \\ &= \fc {a^4} 4 \tan t \sec^3 t - \fc 1 8 a^4 \tan t \sec t - \fc 1 8 a^4 \ln |\sec t + \tan t| + C_1\\ &= \cansw{\fc 1 8 (2x^2-a^2) x\quF - \fc {a^4} 8 \ln |x+\quF| + C} \end{align} \\]

\\[ \begin{align} (58). \cques{\int \fc {\quF} {x^2} \dd x} &= \int \quF \dd \abig(){-\fc 1 x} = -\fc{\quF}x + \int \fc 1 x \dd (\quF)\\ &= -\fc{\quF}x + \int \fc 1 x \cdot \fc {2x \dd x}{2\quF} = -\fc{\quF}x + \int \fc {\dd x}{\quF}\\ &= \cansw{-\fc{\quF}x + \ln|x+\quF| + C} \end{align} \\]

\\[ \begin{align} (51). \cques{\int \fc {\dd x}{x \quF}} & \quFsub \int \fc {a\sec t \tan t}{a\sec t \cdot a\tan t} \dd t = \fc 1 a \int \dd t = \fc t a\\ &= \cansw{\fc 1 a \arccos \fc a {|x|} + C} \end{align} \\]

\\[ \begin{align} (57). \cques{\int \fc{\quF}x \dd x} & \quFsub \int \fc {a\tan t}{a\sec t} \cdot a\sec t\tan t \dd t = a \int (\sec^2 t -1) \dd t = a \tan t - at\\ &= \cansw{\quF - a\arccos \fc a {|x|} + C} \end{align} \\]

\\[ \begin{align} (61). \cques{\int \fc x {\quG} \dd x} &= \int \fc {-\dd(\quGG)}{2\quG} = \cansw{-\quG + C} \end{align} \\]

\\[ \begin{align} (62). \cques{\int \fc x {(\quG)^3} \dd x} &= \int (\quGG)^{-\fc 3 2} \cdot -\dd (\quGG) = \cansw{(\quGG)^{-\fc 1 2} + C} \end{align} \\]

\\[ \begin{align} (69). \cques{\int x\quG \dd x} &= \int (\quGG)^{-\fc 1 2} \cdot -\fc 1 2 \dd (\quGG) = \cansw{-\fc 1 3 (\quGG)^{\fc 3 2} + C} \end{align} \\]

\\[ \begin{align} (59). \cques{\int \fc {\dd x}{\quG}} & \quGsub \int \fc{a\cos t \dd t}{a\cos t} = \int \dd t = t\\ &= \cansw{\arcsin \fc x a + C} \end{align} \\]

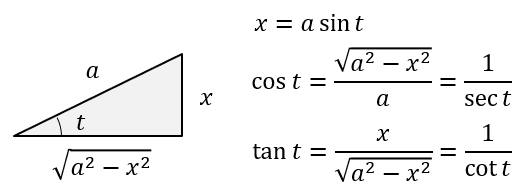
\\[ \begin{align} (60). \cques{\int \fc {\dd x}{(\quG)^3}} & \quGsub \int \fc{a\cos t \dd t}{(a\cos t)^3} = \fc 1 {a^2} \int \sec^2 t \dd t\\ &= \fc 1 {a^2} \tan t + C \cansw{\fc x {a^2 \quG} + C} \end{align} \\]

\\[ \begin{align} (63). \cques{\int \fc {x^2}{\quG} \dd x} & \quGsub \int \fc{a^2\sin^2 t}{a\cos t} a\cos t \dd t = a^2 \int \sin^2 t \dd t\\ &= a^2 \int \fc {1-\cos 2t} 2 \dd t = \fc {a^2} 2 \int \dd t - \fc{a^2} 4 \int \cos 2t \dd (2t) \\ &= \fc {a^2} 2 t - \fc {a^2} 4 2\sin t \cos t + C = \cansw{\fc {a^2} 2 \arcsin \fc x a - \fc 1 2 x \quG + C} \end{align} \\]

\\[ \begin{align} (64). \cques{\int \fc {x^2}{(\quG)^3} \dd x} & \quGsub \int \fc{a^2\sin^2 t}{(a\cos t)^3} a\cos t \dd t = \int \tan^2 t \dd t\\ &= \int \sec^2 t \dd t - \int \dd t = \tan t - t = \cansw{\fc x {\quG} - \arcsin \fc x a + C} \end{align} \\]

\\[ \begin{align} (65). \cques{\int \fc {\dd x}{x\quG}} & \quGsub \int \fc {a\cos t \dd t}{a\sin t \cdot a \cos t} = \fc 1 a \int \csc t \dd t\\ &= \fc 1 a \ln |\csc t - \cot t| + C = \cansw{\fc 1 a \ln \abig||{\fc {a-\quG} x} + C} \end{align} \\]

\\[ \begin{align} (66). \cques{\int \fc {\dd x}{x^2 \quG}} & \quGsub \int \fc {a\cos t \dd t}{a^2 \sin^2 t \cdot a \cos t} = \fc 1 {a^2} \int \csc^2 t \dd t\\ &= -\fc 1 {a^2} \cot t + C = \cansw{-\fc {\quG}{a^2 x} + C} \end{align} \\]

\\[ \begin{align} (67). \cques{\int \quG \dd x} & \quGsub \int a \cos t \cdot a \cos t \dd t = a^2 \int \fc {1+\cos 2t} 2 \dd t \\ &= \fc {a^2} 2 \int \dd t + \fc {a^2} 4 \int \cos 2t \dd (2t) = \text{ref (63).} \\ &= \cansw{\fc {a^2} 2 \arcsin \fc x a + \fc 1 2 x \quG + C} \end{align} \\]

\\[ \begin{align} \int \cos^n \dd x &= \int \cos^{n-1} \dd (\sin x) = \sin x \cos^{n-1} x - \int \sin x \dd (\cos^{n-1} x)\\ &= \sin x \cos^{n-1} x - (n-1)\int \sin x \cos^{n-2} x \cdot -\sin x \dd x\\ &= \sin x \cos^{n-1} x + (n-1) \int \cos^{n-2} x \dd x - (n-1)\int \cos ^n x \dd x \end{align} \\]

\\[ \cansw{\int \cos^n x \dd x = \fc {\sin x \cos^{n-1} x} n + \fc {n-1} n \int \cos ^{n-2} x \dd x} \\]

\\[ \begin{align} (68). \cques{\int (\quG)^3 \dd x} & \quGsub \int a^3 \cos^3 t \cdot a \cos t \dd t = a^4 \int \cos^4 t \dd t\\ &= a^4 \abig(){\fc {\sin t \cos^3 t} 4 + \fc {3\sin t \cos t} 8 + \fc {3t} 8 } + C\\ &= \cansw{\fc {5a^2 - 2x^2} 8 x\quG + \fc 3 8 a^4 \arcsin \fc x a + C} \end{align} \\]

\\[ \begin{align} (70). \cques{\int x^2 \quG \dd x} & \quGsub \int a^2\sin^2 t \cdot a\cos t \cdot a\cos t \dd t = a^4 \int \cos^2 t (1-\cos^2 t) \dd t \\ &= -a^4 \cos^4 t \dd t + a^4 \int \cos^2 t \dd t \\ &= -a^4 \cos^4 t \dd t + \fc {4a^2} 8 x\quG + \fc {4a^4} 8 \arcsin \fc x a \\ &= \cansw{\fc {2x^2-a^2} 8 x\quG + \fc 1 8 a^4 \arcsin \fc x a + C} \end{align} \\]

\\[ \begin{align} (71). \cques{\int \fc {\quG}x \dd x} & \quGsub \int \fc {a\cos t}{a\sin t} a\cos t \dd t = a\int \fc {1-\sin^2 t}{\sin t} \dd t \\ &= a\int \csc t \dd t - a\int \sin t \dd t = \ln |\csc t - \cot t| + \cos t \\ &= \cansw{\quG + a \ln \abig||{\fc {a-\quG} x} + C} \end{align} \\]

\\[ \begin{align} (72). \cques{\int \fc {\quG} {x^2} \dd x} & \quGsub \int \fc {a\cos t}{a\sin t} a\cos t \dd t = \int \cot^2 t \dd t \\ &= \int (\csc^2 t - 1) \dd t = -\cot t - t = \cansw{-\fc {\quG} x - \arcsin \fc x a + C} \end{align} \\]