微积分-泰勒展开式

微积分 / 数学 2023年5月4日
0

泰勒展开式

泰勒展开式的由来

在数学中，加法、减法、乘法和除法是四种最基本、也是最简单的运算。要计算任意复杂的加法、减法、乘法和除法在内的混合运算，只需要熟记九九乘法表，再结合竖式就可以计算得到最终的结果。

多项式函数是由常数和变量之间的加、减、乘以及幂次方运算得到的，它的表达式为：

\\[ a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n + \cdots \\]

多项式函数可以算是比较友好的函数，因为给定一个 \\( x \\) ，可以比较容易地计算出函数的值。而且多项式函数求导、积分运算也非常方便。

但并不是所有表达式的计算都很简单，也不是所有函数的结果都易于求出。在几种初等函数中，三角函数 \\( \sin(x) \\) 就是这样一个例子。虽然有一些特殊情况例如 \\( \sin(\cfrac{\pi}{6})=\cfrac 1 2 \\) ，但是想要求出 \\( \sin(2.36) \\) 这种值，目前似乎并没有一个已知的工具能快速、准确地给出它的精确或近似精确的解。

其余的几个基本函数也存在这种问题，例如对于 \\( e^{7.52} \\) ，这种非整数次幂就很难直接计算出。因此，这些函数虽然性质很简单，但真正需要计算的时候却难以下手。这时候就会想到，这些函数是否能像多项式函数一样，借用基本的四则运算工具就能计算结果。

也就是说，是否有可能存在这样一个多项式函数

\\[ g(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n + \cdots \\]

和一些复杂的函数 \\( f(x) = e^x/\sin x /\cos x \\) 能够相等，或者说至少在某一个范围能至少能近似相等，这样就可以使用多项式函数去计算复杂函数任一点处的值了，就像这样：

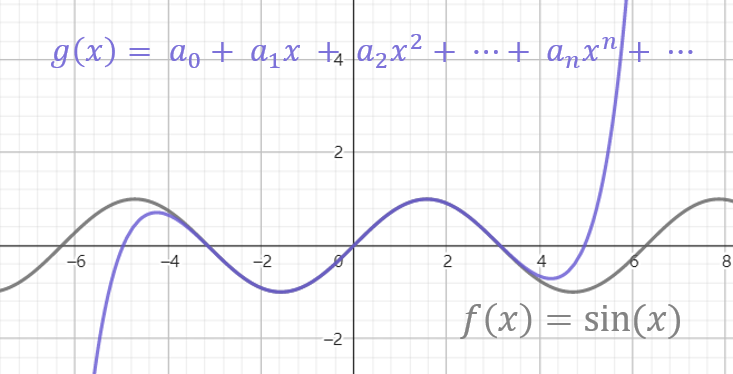
这个多项式函数是 \\( \displaystyle{g(x) = x-\frac 1 6 x^3 + \frac 1 {120} x^5 - \frac 1 {5040} x^7 + \frac 1 {362880} x^9} \\) ，它与 \\( f(x)=\sin(x) \\) 在 \\( [-3,3] \\) 范围内表现出惊人的相似性，\\( f(3) \\) 与 \\( g(3) \\) 的差值只有 \\( 0.0042 \\) ，\\( f(1) \\) 与 \\( g(1) \\) 的差值更是只有 \\( 0.000000025 \\) ，这个精度用于计算已经很高了。

一个四项的多项式函数就能和 \\( \sin(x) \\) 在一定范围内如此接近，有理由相信可能存在一个项数更多的多项式函数，它能在更大的范围内接近 \\( \sin(x) \\) ，或者在此范围内更接近 \\( \sin(x) \\) 甚至完全一致。接下来研究如果这样的多项式函数如果存在，它需要满足怎么样的一个规律或性质。

如果

\\[ \begin{align} g(x) &= a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n + \cdots\\ f(x) &= e^x/\sin x /\cos x/\cdots \end{align} \\]

这两个函数能够相等的话，那么对于定义域内任意一点 \\( x_0 \\) ，总有 \\( f(x_0)=g(x_0) \\) 。

当然，这两个函数不一定能完全相等，不过这两个函数哪怕能在一个点的附近能够近似相等，也非常具有研究价值。\\( x=0 \\) 是一个比较特殊的点，因为该点处 \\( g(x) \\) 除了第一项外其余项的结果都为 \\( 0 \\) ；并且对于函数 \\( f(x)=e^x/\sin x /\cos x \\) 它们在 \\( x=0 \\) 处的值也是容易求得的，分别为 \\( 1/0/1 \\) 。

接下来就以 \\( x=0 \\) 附近为例，研究这两个函数的相等条件。如果这附近能存在 \\( f(x)=g(x) \\) ，它必定要满足以下条件：

\\[ \begin{align} g(0) &= a_0 + a_1 \cdot 0 + a_2 \cdot 0^2 + \cdots + a_n \cdot 0^n + \cdots\\ &= a_0\\ &= f(0) \end{align} \\]

这样就可以解出 \\( a_0 = f(0) \\) 了。

但好像除了 \\( x=0 \\) ，不存在其它的特殊点能够解出其它参数了。不过实际上对 \\( x=0 \\) 这个点的研究并没有结束。\\( f(0)=g(0) \\) 真的能说明两个函数在 \\( x=0 \\) 附近完全一致吗？例如以下两个函数：

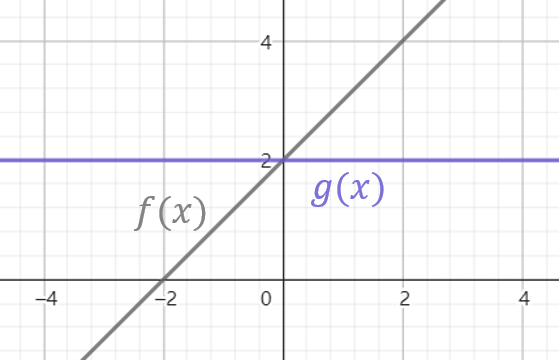
如果只看 \\( x=0 \\) 附近的范围，可以发现两个函数虽然值的大小相近，但是值的变化率或者说函数图像的倾斜程度并不相近，这就会导致 \\( f(x) \\) 和 \\( g(x) \\) 在离开 \\( x=0 \\) 后立刻就不相等了，并且离得越远差异越大。这样就会使得用这个多项式函数计算一个很接近但不完全是 \\( x=0 \\) 附近的函数值，结果和原函数值的差距可能也很大。

说到变化率，很自然就联想到导数。也就是说两者的导函数必须要在 \\( x=0 \\) 处相等，即 \\( g'(0)=f'(0) \\) 。

对于这三个函数 \\( e^x/\sin x /\cos x \\) ，它们的导数分别为 \\( e^x/\cos x /-\sin x \\) 。而它们导数在 \\( x=0 \\) 这一点的值也容易求得，分为为 \\( 1/1/0 \\) 。

而多项式函数 \\( g(x) \\) 的导数为：

\\[ g'(x) = 0 + a_1 \cdot 1 + a_2 \cdot 2 x + a_3 \cdot 3 x^2 + \cdots + a_n \cdot n x^{x-1} + \cdots \\]

容易发现，\\( x=0 \\) 仍然是一个特殊点，该点处 \\( g'(x) \\) 除了第二项外其余项的结果都为 \\( 0 \\) 。也就是说，如果要使 \\( f(x) \\) 和 \\( g(x) \\) 在离开 \\( x=0 \\) 后还能保持一小段距离的相等，它们在 \\( x=0 \\) 的增长率需要一致，也就是说要满足以下条件：

\\[ \begin{align} g'(0) &= 0 + a_1 \cdot 0 + a_2 \cdot 0 + a_3 \cdot 0 + \cdots + a_n \cdot 0 + \cdots\\ &= a_1\\ &= f'(0) \end{align} \\]

不过一阶导数相等还不能说明两者在 \\( x=0 \\) 附近就能完全一致，例如：

可以看到，虽然两者在 \\( x=0 \\) 附近确实保持了一段距离近似相等，但没过一会这个差距又迅速拉开了。这种情况说明两者的变化率虽然在一点处相等，但是凹凸性并不相等，也可以说两者变化率的变化率不等。

说到这两个指标，可以想到二阶导数。也就是说，两者的二阶导函数也需要在 \\( x=0 \\) 处相等。而多项式函数的二阶导数为：

\\[ g''(x) = 0 + 0 + a_2 \cdot 2 + a_3 \cdot 3 \cdot 2 x + \cdots + a_n \cdot n \cdot (n-1) x^{x-2} + \cdots \\]

对于二阶导数，\\( x=0 \\) 处 \\( g''(x) \\) 除了第三项外其余项的结果都为 \\( 0 \\) 。也就是说，如果要使 \\( f(x) \\) 和 \\( g(x) \\) 在离开 \\( x=0 \\) 后增长率保存一致，并且增长率的变化也保持一致，那就要使两者在 \\( x=0 \\) 的加速度相等，即：

\\[ \begin{align} g''(0) &= 0 + 0 + a_2 \cdot 2 + a_3 \cdot 0 + \cdots + a_n \cdot 0 + \cdots\\ &= a_2 \cdot 2\\ &= f''(0) \end{align} \\]

根据这个规律推广下去，如果要让多项式函数和它“模仿”的原函数在 \\( x=0 \\) 附近完全等价，就要求两者在该点处的任意阶导数相等。而这么一直推导下去可以得到如下规律：

\\[ \begin{align} g'''(x) &=6a_3+24a_4x+60x^2+ \cdots +n(n-1)(n-2)x^{n-3}+ \cdots = f'''(x) \\ g^{(4)}(x) &=24a_4+120x+ \cdots +n(n-1)(n-2)(n-3)x^{n-4}+ \cdots = f^{(4)}(x) \\ &\vdots\\ g^{(n)}(x) &=n!a_n + (n+1)!a_{n+1}x + \cdots = f^{(n)}(x) \end{align} \\]

如果要使两者在 \\( x=0 \\) 附近完全等价，那么令各式中的 \\( x=0 \\) ，就有如下规律：

\\[ \begin{align} g(0) &= a_0 = f(0) \\ g'(0) &= a_1 = f'(0) \\ g''(0) &= 2a_2 = f''(0) \\ g'''(0) &= 6a_3 = f'''(0) \\ g^{(4)}(0) &= 24a_4 = f^{(4)}(0) \\ &\cdots \\ g^{(n)}(0) &= n!a_n = f^{(n)}(0) \end{align} \\]

也就是说，通过每一阶的导数，都可以解出多项式每一项的系数：

\\[ a_0=f(0) \quad a_1=\frac{f'(0)}{1!} \quad a_2=\frac{f''(0)}{2!} \quad a_3=\frac{f'''(0)}{3!} \quad \cdots \quad a_n=\frac{f^{(n)}(0)}{n!} \\]

于是，可以得到 \\( f(x) \\) 在 \\( x=0 \\) 处的展开式：

\\[ \begin{align} f(x) &= g(x)\\ &=\frac{f(0)}{0!}+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3 + \cdots + \frac{f^{(n)}(0)}{n!}x^n + \cdots \end{align} \\]

以上公式称为麦克劳林(Maclaurin)展开式。麦克劳林展开式表明如果要用一个多项式函数和一个任意复杂的函数在 \\( x=0 \\) 处完全等价，那么这个多项式函数是什么。

该展开式有一个缺点，就是只能用于计算 \\( x=0 \\) 附近等价的多项式，而对其它点不适用；而且如果 \\( f(x) \\) 在 \\( x=0 \\) 处没有定义或不可导，那么麦克劳林展开式似乎就失效了。

不过这个缺点也很好解决：如果函数 \\( f(x) \\) 在 \\( x=x_0 \\) 处任意阶可导，只需把该函数平移到原点就可以应用麦克劳林展开式。\\( f(x) \\) 向左平移 \\( x_0 \\) 距离的结果为 \\( f(x-x_0) \\) ，就是把所有的 \\( x \\) 改写成 \\( x-x_0 \\) 的方式。这便是泰勒(Taylor)展开式的一般形式：

\\[ \begin{align} f(x)&=g(x)\\ &=f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\frac{f'''(x_0)}{3!}(x-x_0)^3 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + \cdots \end{align} \\]

佩亚诺余项

当对函数应用泰勒展开式时，它只有展开项数趋于无穷时，两者才能在某点附近完全相等。但无穷项根本不可能用于计算，实际中总是希望只使用一个有限的多项式

\\[ p(x)=f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(0)}{2!}(x-x_0)^2+ \cdots + \frac{f^(n)(0)}{n!}(x-x_0)^n \\]

来表示它。其余被忽略的部分称为余项，记作 \\( R(x) \\) 。因此一个函数的展开式也可以表示为多项式和余项之和 \\( f(x)=p(x)+R(x) \\) 。

注意到泰勒展开的一个特点是，展开越多，项的次数越大，余项的次数全都比多项式的次数大，因此余项在 \\( x_0 \\) 附近，它收敛到 0 的速度要远比多项式快，即：

\\[ \lim_{x \to x_0} \frac{R(x)}{p(x)} =\lim_{x \to x_0} \cfrac{ \cfrac{f^{(n+1)}(x_0)}{(n+1)!}(x-x_0)^{n+1}+\cfrac{f^{(n+2)}(x_0)}{(n+2)!}(x-x_0)^{n+2}+\cdots }{ \cfrac{f^{(n)}(0)}{n!}(x-x_0)^n + \cfrac{f^{(n-1)}(0)}{(n-1)!}(x-x_0)^{n-1} +\cdots }=0 \\]

使用洛必达法则也很容易求解这个极限。所以佩亚诺(Peano)余项将其表示为一个高阶无穷小 \\( R(x)=o((x-x_0)^n) \\) 。

泰勒展开式的项是无限多的，而佩亚诺余项则引入了“精度”这一概念：可以根据外界环境精度的要求，决定需要展开到几项多项式，后续的部分则可以省略。这就像将一个无限小数四舍五入到某一位一样。

例如，假设要求以下极限的值：

\\[ \lim_{x \to 0} \frac{\tan x - x}{x^3} \\]

这里的精度要求是 \\( x^3 \\) ，更高次的项可以忽略，那么可以将 \\( \tan x \\) 在 \\( x=0 \\) 展开为带有佩亚诺余项的多项式：

\\[ (x\to 0) \quad \tan x = x + \frac{x^3}{3} + o(x^3) \\]

这时极限的结果就非常容易求得了：

\\[ \begin{align} \lim_{x \to 0} \frac{\tan x - x}{x^3} &= \lim_{x \to 0} x + \cfrac{x + \cfrac{x^3}{3} + o(x^3) - x}{x^3}\\ &= \lim_{x \to 0} \frac{x^3}{3 \cdot x^3} = \frac 1 3 \end{align} \\]

拉格朗日余项

佩亚诺余项使用无穷小的方式来表示余项，这样做虽然简单直接，在很多计算极限问题中很有用，但它终究还是回避了“余项到底有多大”这个主题，这就使得当 \\( x \\) 稍微远离 \\( x_0 \\) 时，佩亚诺余项不能用于估算有限的多项式和原函数的误差。

在之前的学习中，已经知道了柯西中值定理。如果 \\( f(x) \\) 在 \\( [x_1,x_2] \\) 内连续，在 \\( (x_1,x_2) \\) 内可导且 \\( g(x) \\) 的导数不为 0 ，则有：

\\[ \frac{f(x_1)-f(x_2)}{g(x_1)-g(x_2)}=\frac{f'(\xi)}{g'(\xi)} \\]

其中 \\( \xi \\) 是介于 \\( x_1 \\) 与 \\( x_2 \\) 之间的某个值。

柯西中值定理的几何解释就是，由 \\( x \\) 引导的参数方程确定的曲线，任取其中光滑的某一段，这段内一定有一点的切线斜率和两端的斜率相等：

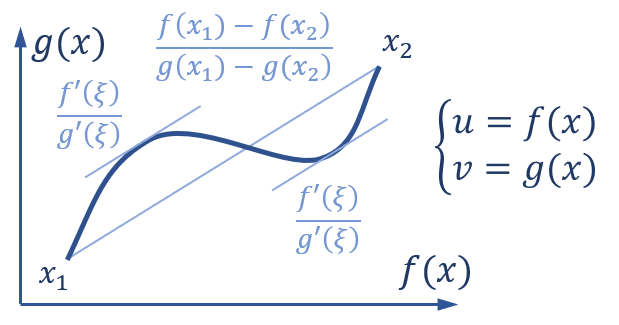
而泰勒公式的余项为：

\\[ R(x) = \frac{f^{(n+1)}(x_0)}{(n+1)!}(x-x_0)^{n+1}+\frac{f^{(n+2)}(x_0)}{(n+2)!}(x-x_0)^{n+2}+\cdots +\frac{f^{(\infty)}(x_0)}{(\infty)!}(x-x_0)^{\infty}\\ \\]

余项中的每项都不一样，不过它们都有 \\( S(x) = (x-x_0)^{n+1} \\) 这个公因式。为了方便分析，可以先将这些公因式去除：

\\[ \frac{R(x)}{S(x)} \\]

不过先不急着展开，分子分母这两个函数都有一个点比较特殊，就是 \\( x=x_0 \\) ：在 \\( x=x_0 \\) 处，有 \\( R(x)=S(x)=0 \\) ，所以可以应用柯西中值定理：

\\[ \frac{R(x)}{S(x)}=\frac{R(x)-R(x_0)}{S(x)-S(x_0)}=\frac{R'(\xi)}{S'(\xi)} \\]

其中 \\( \xi \\) 为介于 \\( x \\) 和 \\( x_0 \\) 的某个值。这样便可以使用这两个多项式等价之前的余项和公因式：

\\[ \begin{align} R'(\xi) &= \frac{f^{(n+1)}(x_0)}{(n)!}(\xi-x_0)^{n}+\frac{f^{(n+2)}(x_0)}{(n+2)!}(\xi-x_0)^{n+1}+\cdots \\ S'(\xi) &= (n+1)(\xi-x_0)^{n} \end{align} \\]

因为 \\( \xi \\) 可能是介于 \\( x \\) 和 \\( x_0 \\) 的任意值，因此这两个多项式可以看作关于 \\( \xi \\) 的函数。而它们在 \\( \xi=x_0 \\) 处，仍有：\\( R'(\xi)=S'(\xi)=0 \\) ，故上式仍然可以运用柯西中值定理：

\\[ \frac{R'(\xi)}{S'(\xi)}=\frac{R'(\xi)-R'(x_0)}{S'(\xi)-S'(x_0)}=\frac{R''(\xi_2)}{S''(\xi_2)} \\]

其中 \\( \xi_2 \\) 为介于 \\( \xi \\) 和 \\( x_0 \\) 之间的某个值。考虑到 \\( \xi \\) 是介于 \\( x \\) 和 \\( x_0 \\) 之间的某个值，实际上 \\( \xi_2 \\) 也是这个范围内的值。

像这样多次应用柯西中值定理，可以得出：

\\[ \frac{R(x)}{S(x)}=\frac{R'(\xi)}{S(\xi)}=\frac{R''(\xi_2)}{S''(\xi_2)}=\cdots= \frac{R^{(n+1)}}{S^{(n+1)}}=\frac{R^{(n+1)}(\xi_{n+1})}{(n+1)!} \\]

柯西中值定理是一个将函数与导数相关联的定理。对多项式求导是一种降低次数的过程：因为 \\( R^{(n+1)}(x)=f^{(n+1)}(x)-p^{(n+1)}(x) \\) ，而 \\( p(x) \\) 的最高次为 \\( n \\) ，所以经过 \\( n+1 \\) 次求导，多项式 \\( p^{(n+1)}(x)=0 \\) ，这种情况下 \\( R^{(n+1)}(x)=f^{(n+1)}(x) \\) ，余项将决定原函数的走向，所以有 \\( R^{(n+1)}(\xi)=f^{(n+1)}(\xi) \\) 。整理得

\\[ R(x)=\frac{R^{(n+1)}(\xi_{n+1})}{(n+1)!}S(x)=\frac{f^{(n+1)}(\xi_{n+1})}{(n+1)!}(x-x_0)^{n+1} \\]

其中 \\( \xi_{n+1} \\) 为介于 \\( x \\) 与 \\( x_0 \\) 之间的某个值。以上的余项记作 \\( R_n(x) \\) ，称作拉格朗日(Lagrange)余项。

拉格朗日余项表明，如果以多项式 \\( p(x) \\) 近似表达函数 \\( f(x) \\) 时，两者的误差为 \\( |R_n(x)| \\) 。如果多项式的最高项 \\( n \\) 是确定的，在 \\( x \\) 与 \\( x_0 \\) 范围内函数 \\( n+1 \\) 阶导数的界限 \\( |f^{(n+1)}(x)| \le M \\) 已知，那么误差的估计式为：

\\[ |R_n(x)| \le \frac{M}{(n+1)!}|x-x_0|^{n+1} \\]

利用以上估计式，就可以得知利用有限项多项式计算的精度，这在数值计算时很有用。

泰勒展开与级数

通过之前对泰勒展开式的介绍可以知道，泰勒展开式使用多项式在某点附近模拟一个函数。例如，\\( \sin x \\) 在 \\( x=0 \\) 附近的展开式（麦克劳林展开）为：

\\[ \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} + \dots + \frac{(-1)^n x^{2n+1}}{(2n+1)!} \\]

绘制 \\( \sin x \\) 逐项展开后的函数图像如下：

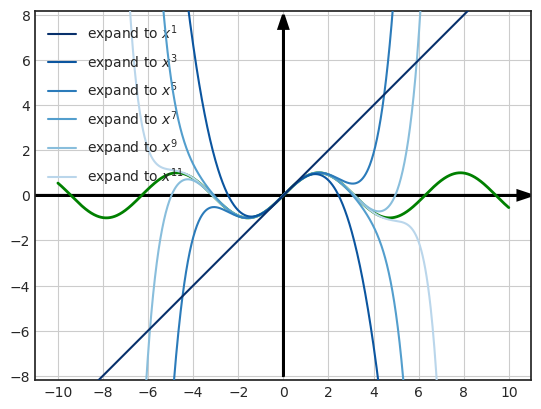
观察以上展开式可以发现，随着展开的项数越来越多，多项式向着两侧越来越贴合正弦函数的形状，这就像逐渐将一根铁丝掰成波浪线的过程。

接下来考虑泰勒展开式在 \\( x_0 \\) 附近多大的范围（邻域）上能和原函数相等。

泰勒展开式是无穷多个幂函数之和，因此它是一个无穷级数，还是一个幂级数。因此泰勒展开式也可以写作：

\\[ f(x)=\sum\limits_{n=0}^{\infty}\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n} \\]

对于一个级数，首先要考虑的就是它的收敛性。如果一个级数都不收敛，那么就没有讨论的必要了。

幂级数收敛性有一个很重要的定理：对于形如 \\( \displaystyle \sum_{n=0}^{\infty} a_n(x-x_0)^n \\) 的幂级数，若 \\( \displaystyle \lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\frac 1 R \\) ，则该幂级数在 \\( |x-x_0|\lt R \\) 上是收敛的，至于边界上的收敛情况要单独讨论。

而泰勒展开的幂级数通项为：

\\[ P_{n}(x)=\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n} \\]

因此，泰勒级数的收敛半径为：

\\[ R=\lim_{n\to\infty}\left|\frac{a_n}{a_{n+1}}\right|=\lim_{n\to\infty}\left|\frac{(n+1)f^{(n)}(x_0)}{f^{(n+1)}(x_0)}\right| \\]

例如，对于 \\( e^x \\) 的泰勒展开，它的每一阶导数都是相同的，这就有：

\\[ R=\lim_{n\to\infty}\left|\frac{a_n}{a_{n+1}}\right|=\lim_{n\to\infty}\left|\frac{(n+1)e^{x_0}}{e^{x_0}}\right|=\lim_{n\to\infty}|n+1|=\infty \\]

这说明对 \\( e^x \\) 展开后的泰勒级数在 \\( \mathbb{R} \\) 上全部收敛，展开式对任何 \\( x \\) 都能计算出一个值。

既然泰勒展开的级数在这些范围内收敛，接下来看看它到底收敛到什么程度。以 \\( \sin x \\) 为例，它在 \\( x=0 \\) 处展开后，其展开式在任意 \\( x \\) 处的拉格朗日余项为：

\\[ R(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} \\]

\\( x \\) 的各阶导数导来导去就是 \\( \pm\sin x \\) 或 \\( \pm\cos x \\) 中的一个，因此导数这部分产生的误差为 \\( f^{(n+1)}(\xi) \le 1 \\) ，所以余项的误差界限为：

\\[ |p(x) − \sin(x)| \le \frac{|x|^{n+1}}{(n+1)!} \\]

如果让原函数展开到无限多项，那么误差就逐渐趋于以下值：

\\[ \lim_{n\to\infty} \frac{|x|^{n+1}}{(n+1)!} \\]

对于这个极限，可以这样理解：分子和分母都是 \\( n+1 \\) 个数相乘，但对于 \\( |x|^{n+1} \\) 来说，每个相乘的数都是 \\( x \\) ，是不变的；但 \\( (n+1)! \\) 随着 \\( n \\) 的无止境上升，总有那么一刻 \\( n \\) 的大小会超过 \\( x \\) 的大小，在这之后 \\( (n+1)! \\) 将很快追平并超过 \\( |x|^{n+1} \\) ，并且随着 \\( n \\) 的无限增长，这个差距将无限扩大。因此，原极限将趋于 0 ：

\\[ \lim_{n\to\infty} \frac{|x|^{n+1}}{(n+1)!}=0 \\]

余项趋于 0 ，这说明 \\( \sin x \\) 展开的泰勒级数不仅在 \\( \mathbb{R} \\) 内收敛，并且在这个范围内还和原函数相等。

这个结论初看有点难以置信，泰勒展开只通过了一点上的多项式展开，却得到了整个实数范围的函数趋近。对于这个问题的理解：在一点处无穷多阶导数的信息实在是太丰富了，通过一阶导数，能预测到函数在下一个微小范围内的变化；通过二阶导数能预测到一阶导数在下一个微小范围内的变化，从而预测函数在下下个微小范围内的变化，……。这样无限多的信息便有可能预测到函数在整个实数范围的走势。

泰勒展开的应用非常广泛，除了求解极限问题外，泰勒展开常用于函数值以及积分和微分方程的近似计算。除此之外，利用复数域中的泰勒展开可以发现许多特别的性质。例如，对 \\( e^{ix} \\) 的展开等价于 \\( \cos x+ i\sin x \\) 的展开，代入 \\( x=\pi \\) 就可以得到著名的欧拉公式 \\( e^{i\pi}+1=0 \\) 。

附录

常用函数的麦克劳林展开

以下列出了常用函数的麦克劳林展开式，通过将 \\( x \\) 改写为 \\( x-x_0 \\) 便可以得到对应的泰勒展开式。

\\[ \begin{align} (1)&\quad e^x =1+x+\frac{x^2}{2!}+\cdots+\frac{x^n}{n!}+\cdots &&=\sum_{n=0}^{\infty}\frac{x^n}{n!} && x \in \mathbb{R}\\ (2)&\quad \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} + \dots + (-1)^n\frac{x^{2n+1}}{(2n+1)!}+\cdots &&=\sum_{n = 0}^{\infty} (-1)^n \frac{x^{2n+1}}{(2n+1)!} && x \in \mathbb{R}\\ (3)&\quad \cos x =1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots+(-1)^n\frac{x^{n+1}}{n+1}+\cdots &&=\sum_{n=0}^{\infty}(-1)^n \frac{x^{2n}}{(2n)!} && x \in \mathbb{R}\\ (4)&\quad \ln (1+x) =x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots+(-1)^n\frac{x^{n+1}}{n+1}+\cdots &&=\sum_{n=1}^{\infty} (-1)^{n-1} \frac{x^n}{n} && -1 < x \le 1\\ (5)&\quad \frac{1}{1-x} =1+x+x^2+x^3+\cdots+x^n &&=\sum_{n=0}^{\infty} x^n && -1<x<1\\ \end{align} \\]

参考资料/延伸阅读

https://www.bilibili.com/video/av11251323
3b1b 对泰勒展开式的介绍

https://www.ixigua.com/6577670049224458765
https://www.ixigua.com/6578415087093023239
妈咪叔对泰勒展开式的介绍

You may also like...

发表回复

您的电子邮箱地址不会被公开。 必填项已用*标注

活动日历

2023年 6月
一 二 三 四 五 六 日
 1234
567891011
12131415161718
19202122232425
2627282930  

音频

京ICP备2021034974号
contact me by hello@frozencandles.fun