机器学习-朴素贝叶斯

贝叶斯分类器

算法原理

贝叶斯分类源自概率论上著名的贝叶斯定理(Bayes's theorem)。设某事件的样本空间为 \\( S \\) ，事件 \\( A \\) 与 \\( B \\) 为 \\( S \\) 中的两个事件，则为事件 \\( B \\) 发生的条件下事件 \\( A \\) 发生的概率可以使用如下的贝叶斯公式计算：

\\[ P(A|B) = \frac{P(B|A)P(A)}{P(B)} \\]

该公式可以结合以下 Venn 图理解，注意 \\( P(B|A) = \displaystyle{\frac{P(A \cap B)}{P(A)}} \\) ：

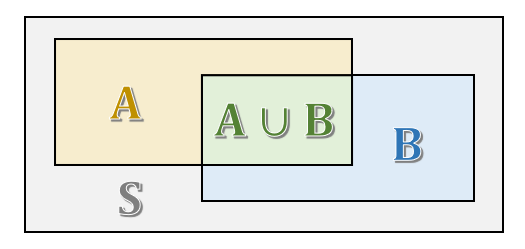
贝叶斯公式的用途为：很多时候并不能直接得出在事件 \\( B \\) 发生的情况下事件 \\( A \\) 发生的概率，但是根据贝叶斯公式，可以采用一种迂回的方式计算出它的概率。

接下来看一个示例。假设研究人员统计了 10000 份邮件，其中包含 1500 份垃圾邮件，发现垃圾邮件中有 30% 的邮件都包含单词“ sale ”，而非垃圾邮件中只有 1% 包含该单词。如果现在新收到了一份邮件，它包含该单词，问它是垃圾邮件的概率。

这种问题直接分析较难，但借助贝叶斯公式可以根据已有条件计算。设事件 \\( X1 \\) 为一封邮件是垃圾邮件，\\( X2 \\) 为是普通邮件，\\( Y \\) 为包含该关键词的邮件，则 \\( X1 \cup X2=S , X1 \cap X2= \varnothing \\) ，那么有：

\\[ P(X_1) = 0.15, P(X_2) = 0.85, P(Y|X_1) = 0.3, P(Y|X_2) = 0.01 \\]

由贝叶斯公式，可以完成如下计算：

\\[ P(X_1|Y) = \frac{P(Y|X_1)P(X_1)}{P(Y)} = \frac{P(Y|X_1)P(X_1)}{P(X_1)P(Y|X_1)+P(X_2)P(Y|X_2)} = \frac{90}{107} \approx 84.11 \% \\]

结果显示这封邮件有很高的概率是垃圾邮件，那么它更应该被归入垃圾邮件的分类中。

从计算过程中可以看到，虽然直接分析包含“ sale ”单词的邮件是垃圾邮件的概率较难，但是邮件中垃圾邮件和非垃圾邮件的概率是很方便统计的，而两种邮件的词频也是很好统计的，这些根据以往样本就可以计算得到的概率称为先验概率(prior probability)；而与之相对的后验概率(posterior probability)表示某个已经发生的事件应该发生的概率。容易看出，贝叶斯公式是一种用先验概率计算后验概率的公式。

朴素贝叶斯

在实际问题中，问题的特征变量往往不止一个。不过贝叶斯公式也可以推广至 \\( n \\) 个特征变量，如果某个发生的事件其中每个特征变量的取值情形为 \\( X_1, X_2, \dots, X_n \\) 时，那么贝叶斯公式可以做如下推广：

\\[ P(Y|X_1, X_2, \dots, X_n) = \frac{P(X_1, X_2, \dots, X_n | Y) \cdot P(Y)}{P(X_1, X_2, \dots, X_n)} \\]

它的本质和单个特征变量的贝叶斯公式是一致的。

朴素(naive)贝叶斯模型则假设各个特征变量间相互独立，互不影响，那么该组合概率可以拆分成多个独立概率的积，即可以对上式做如下简化：

\\[ P(X_1, X_2, \dots, X_n) = P(X_1) \cdot P(X_2) \cdots P(X_n) \\]

\\[ P(X_1, X_2, \dots, X_n|Y) = P(X_1 | Y) \cdot P(X_2 | Y) \cdots P(X_n | Y) \\]

这样就将一个复杂的组合概率拆分成多个简单概率的运算。这些简单的概率都易于统计，那么根据贝叶斯公式，就可以计算在 \\( n \\) 个特征变量取不同值的情况下，目标变量为某个分类的概率，并将样本归入概率更高的分类中。

稍后会介绍朴素贝叶斯的应用。

高斯朴素贝叶斯

贝叶斯公式只能计算离散数据的概率，但对连续数据的分类比较困难。例如，对于以下在平面中分布的二维数据：

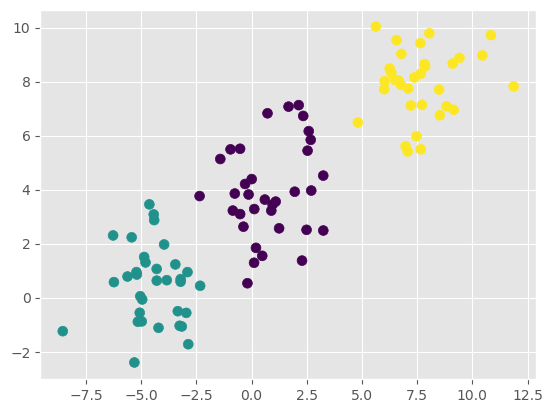
无法用传统的方式来描述样本的概率。不过如果可以假设数据服从高斯分布（正态分布），且各个特征变量间线性无关，那么就可以使用正态分布的概率公式来描述它：

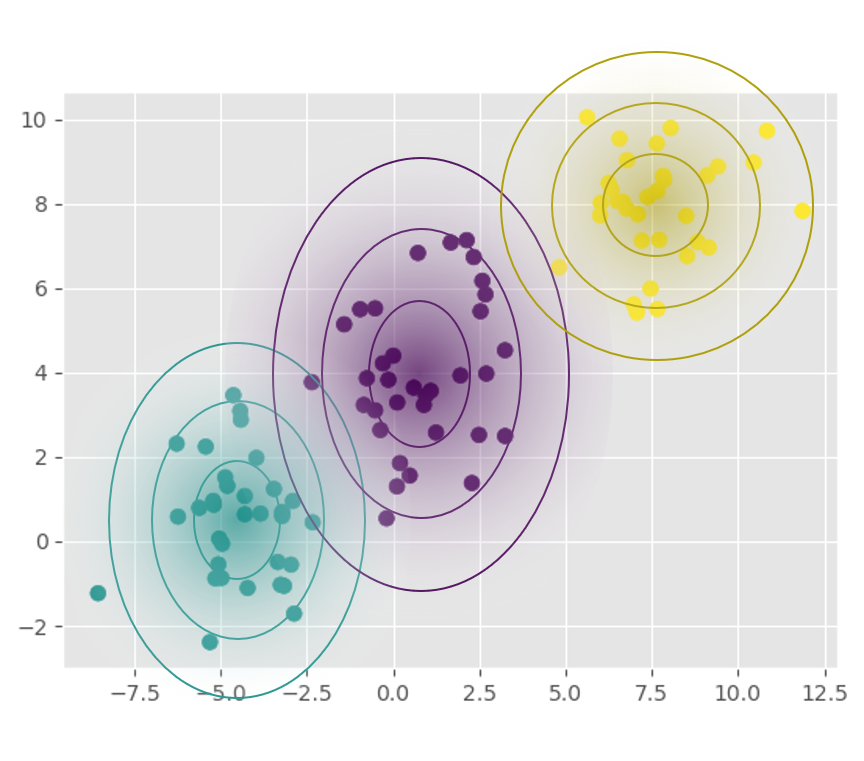
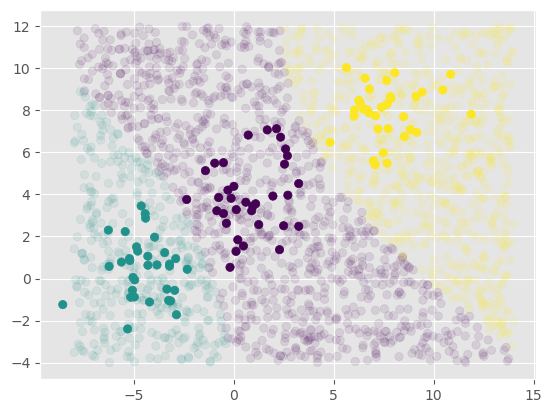
\\[ P(X) = \frac{1}{\sqrt{2 \pi}\sigma}{\large{e}}^{\displaystyle{-\frac{(x-\mu)^2}{2\sigma ^2}}} \\]

每个分类包含样本的均值和标准差很容易计算，代入公式就可以得出先验概率。下图展示了每一类样本的概率密度以及类别间的决策边界：

高斯朴素贝叶斯在 Scikit-Learn 中的实现遵循相同的接口，并且贝叶斯模型几乎没有什么可以调整的参数：

from sklearn.naive_bayes import GaussianNB

model = GaussianNB()

model.fit(X, y_true)

GaussianNB()

当训练完高斯朴素贝叶斯模型后，可以通过 .theta_ 和 .var_ 属性检查每个类别每个特征变量的均值和方差：

model.theta_[0]  # mu (mean)
array([0.82083046, 3.94121607])
model.var_[0]   # sigma ** 2 (variance)
array([2.05995969, 2.92921668])

贝叶斯分类的一个特点是可以直接得出样本属于每一类的概率（概率分类）而不是只给出分类结果，这样有助于判断落在分类边界上的样本。预测分类概率可以通过 .predict_proba() 方法实现：

model.predict_proba([[-2, 2], [5, 4]])
array([[4.23140192e-01, 5.76859808e-01, 5.44257518e-14],
       [9.02345446e-01, 6.10995956e-13, 9.76545538e-02]])

接下来通过一个具体的示例说明朴素贝叶斯分类的应用。

示例：垃圾邮件检测

本节将使用朴素贝叶斯算法将邮件分为普通邮件和垃圾邮件，所使用的数据集可以在 http://archive.ics.uci.edu/ml/machine-learning-databases/00228/ 处下载。由于这里只有英文的数据，因此只能用作英文邮件分类。（中文邮件的分类思路也是一致的，只不过需要更复杂的预处理而已）

这些数据的结构如下：

mail = pd.read_table('dataset/SMSSpamCollection', names=['label', 'text'])
mail.head(3)

            labeltext
        
            0hamGo until jurong point, crazy.. Available only ...
        
            1hamOk lar... Joking wif u oni...
        
            2spamFree entry in 2 a wkly comp to win FA Cup fina...

	label	text
0	ham	Go until jurong point, crazy.. Available only ...
1	ham	Ok lar... Joking wif u oni...
2	spam	Free entry in 2 a wkly comp to win FA Cup fina...

在介绍数据具体的应用之前，先介绍数据

数据预处理：词袋模型

在使用朴素贝叶斯模型来判断一封邮件是否是垃圾邮件前，需要提取自变量的特征，以确定公式的具体组成。

本次提取的文本特征为单词出现的频率，并使用词频计算贝叶斯模型中的概率。可以使用词袋模型(bag-of-words)来处理文本。词袋模型是一种基于词频的文本表示方法，它忽略了词的顺序，只考虑词在文本中出现的次数。词袋模型将所有样本中出现过的特征词汇表汇总成一个向量，每个词汇对应一个维度。

例如，对于以下的文本数据：（示例来自维基百科）

texts = ['John likes to watch movies. Mary likes movies too.',

'Mary also likes to watch football games.']

那么所有的单词可以构成如下形式的词袋：

    ["also", "football", "games", "john", "likes", "mary", "movies", "to", "too", "watch"]

每个文本数据都可以使用这样一个向量的形式来表示，向量上每个维度的值为该文本中对应单词的出现频率。例如，以上第一条文本就可以表示为如下向量：

also	football	games	john	likes	mary	movies	to	too	watch
0	0	0	1	2	1	2	1	1	1

词袋模型是自然语言处理(NLP)中最基础的一种特征提取方法，它仅考虑词频，而忽略了词语的出现位置、先后关系、词性等其它特征。尽管如此，作为一种易于使用且确实能反映文本部分特征的模型，词袋模型在文本分类、情感分析等领域仍有着广泛的应用。

在 Scikit-Learn 内，词袋模型由以下类提供处理方法：

from sklearn.feature_extraction.text import CountVectorizer
count_vect = CountVectorizer()

通过 .fit() 方法可以将其应用于数据集中。可以使用 .vocabulary_ 属性检查当前模型的词典及与向量维度的映射关系：

count_vect.fit(texts)
count_vect.vocabulary_
{'john': 3, 'likes': 4, 'to': 7, 'watch': 9, 'movies': 6, 'mary': 5, 'too': 8, 'also': 0, 'football': 1, 'games': 2}

接下来使用一个具体的样本来演示词袋模型的特征提取结果：

vec = count_vect.transform([
    'Tim likes to play games and watch baseball games.'])
pd.DataFrame(vec.toarray(), columns=count_vect.get_feature_names_out())

            alsofootballgamesjohnlikesmarymoviestotoowatch
        
            00020100101

	also	football	games	john	likes	mary	movies	to	too	watch
0	0	0	2	0	1	0	0	1	0	1

多项式朴素贝叶斯

一段文本的词频并不只有 0 和 1 两种情况，不能直接计算概率，但是可以假定词频服从多项式分布。多项式分布是二项分布的扩展，试验结果不是两种状态，而是多种互斥的离散状态。多项式分布可以描述样本出现次数的概率，因此多项式朴素贝叶斯非常适合用于特征为出现次数或者出现次数比例的情况。

首先使用词袋模型处理数据：

from sklearn.feature_extraction.text import CountVectorizer

count_vect = CountVectorizer(stop_words='english')
X = count_vect.fit_transform(mail['text'])

然后将其应用于多项式朴素贝叶斯模型中：

from sklearn.naive_bayes import MultinomialNB

model = MultinomialNB()

model.fit(X, mail['label'])

MultinomialNB()

根据朴素贝叶斯模型，可以使用词频计算出不同分类下的先验概率，从而计算新的词频向量的分类概率，并将其分到概率更大的一类。以下是一个预测示例，可以看到多项式朴素贝叶斯模型成功地发现了垃圾邮件：

model.predict(
    count_vect.transform(
        ['Interested in trying out our product? '
         'Here’s a special deal for newsletter subscribers: '
         'get 1 years of it with 3 months of extra subscription time added on top.'])
)
array([1], dtype=int64)

总的来说，朴素贝叶斯模型是一种简单的分类算法，并且有坚实的数学原理支撑。朴素贝叶斯模型的一个显著的优点是只需要统计概率，因此计算速度很快，通常适用于维度非常高的数据集。并且由于可调参数很少，可以快速得到最终的结果，因此非常适合作为处理分类问题的基本方案，在得到数据后便可以使用朴素贝叶斯模型得到粗糙的结果。