优先队列的概念
优先队列的概念可以由队列引出。队列可以让先到达的元素先处理,适用于很多需要边处理边容纳新元素的场合。
然而,队列的处理过程也有一些不足:队列只能按顺序逐个处理,此时如果新入队了一个需要紧急处理的元素,队列不允许它插队,只能排队等待处理。
优先队列(priority queue)是一种特殊的队列,它可以像队列一样插入与删除元素,不过它的特点是只能删除队列中的最小值(或者说优先级最高的元素)。这样,通过调整每一个入队元素的优先级,就可以自行调控出队的顺序。
二叉查找树是有序的,可以快速找到最小值,因此可以用于实现优先队列。然而如果直接将二叉树作为优先队列,它支持了太多不必要的操作使得运行速度可能较慢。并且如果要频繁地删除最小值时,二叉查找树需要从左向右删除,那么整棵树就会变得不平衡,还需要做额外的调整。
接下来介绍的优先队列数据结构使用了二叉树的思想,不过它是一棵特别地二叉树,可以更好地实现优先队列。
二叉堆
二叉堆的概念
二叉堆(binary heap)是一棵被完全填满的二叉树,这种二叉树除了最底层外,所有位置都有元素;最底层元素从左到右填入,如下所示:
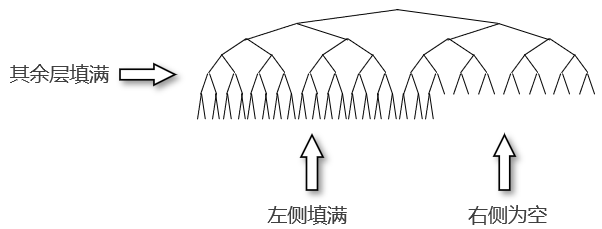
这种二叉树称为完全二叉树(complete binary tree),非常适合用于实现优先队列,甚至“堆”在数据结构中多用于指代优先队列。因为完全二叉树很紧凑,因此可以使用数组表示:对于数组中位置 \\( i \\) 上的元素,它的左侧子节点在位置 \\( 2i \\) 处,右侧子节点在随后的位置 \\( 2i+1 \\) 处。下图说明了数组表示完全二叉树的基本原理:
因此,二叉堆的类型声明如下:
使用数组表示完全二叉树不需要指针,并且可以很容易地遍历树;不过这种情况下树的大小需要提前估计。当然普通的二叉树也可以这么表示,但是普通的二叉树比较散,许多节点(尤其是中间位置的节点)都是空的,使用数组存储还需要给空的节点也预留所有后代的位置,存储效率不高。
二叉堆的堆序性质
二叉堆的一个重要的性质是堆序(heap order),堆序使堆的最小值可以被快速找到。因此,最小值应该被放在堆(数组)的最前面。同时为了使子树也是一个二叉堆这种递归性质,那么任意节点都应该小于它的所有后代元素。
下图展示了一个二叉堆的树状结构:
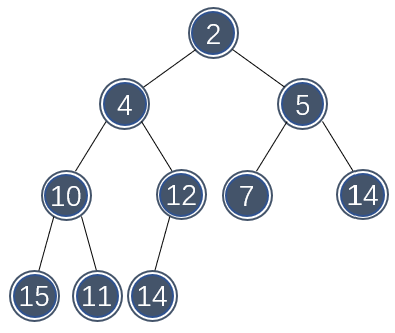
因此,二叉堆的创建过程如下:
注意,使用数组创建二叉堆时,其首位置将空缺出来,使剩下的元素可以直接使用下标值找到对应的父/子节点。
首先研究二叉堆的插入。由于二叉堆是一棵数组描述的完全二叉树,因此为了将一个元素插入到堆中,需要在数组的后一个空闲位置分配一个空闲项。同时,待插入元素可能比该位置的父元素小,不满足二叉堆的定义,需要将该元素与其父元素调换位置。
例如,如果要向以下二叉堆插入元素 3 ,那么首先需要分配一个额外的位置:
为了直观起见,这里将二叉堆绘制成树状结构,但是底层实现依然使用数组。
如果向该位置直接插入 3 ,不符合二叉堆的定义,需要将该位置向上提一层,并与上层的位置对调:
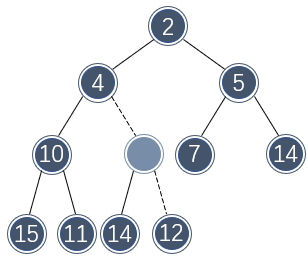
该位置还是不符合二叉堆的定义,还需要再向上提一层:
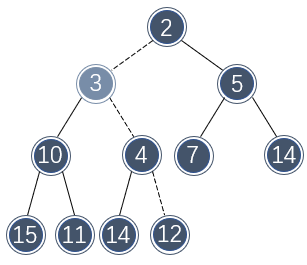
此时,向该位置插入 3 便满足二叉堆的定义了。这种插入策略称为上浮或向上渗透(percolate up)。其代码实现如下:
注意,在插入时可能会一直浮到顶端,此时应该退出循环,否则它还会向索引值为 0 的位置继续移动,甚至造成无限循环。在创建二叉堆时可以通过在 0 号位置放入一个很小的元素,例如 INT_MIN 来避免这一点,同时简化代码的实现。
和插入相反的过程是删除,优先队列只允许删除最小值。最小值默认出现在树的根部,删除该值很快也很容易,但还需要对数组做一定调整使其符合二叉堆的堆序性质。
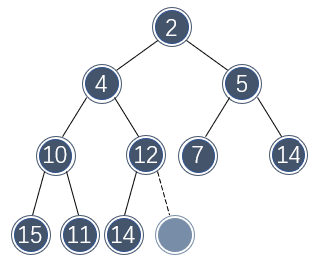
例如,假设需要从以上二叉堆中删除最小值:
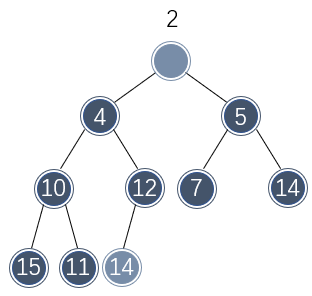
那么肯定要移除树根位置的元素。为了维持堆序性质,需要有其余位置的元素来填补该空缺,不管什么位置的元素来填补该空缺,数组少了一个元素因此最后一个位置必须被释放,该位置的元素必须被移动。
不过该位置的元素不能直接移动到树根处,否则便违背了二叉堆的大小关系。只有树根的两个子节点的元素才能直接移动到树根处。由于左侧节点的值较小,因此移动到树根处不破坏二叉堆的性质:
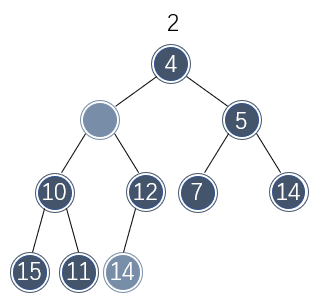
此时又产生了一个空缺位置,并且最后一个位置的元素还是不能直接移到该空缺处。因此再重复几次以上的步骤:将较小的子节点的值移到空缺处,然后观察最后位置的元素是否适合移动到空缺处:
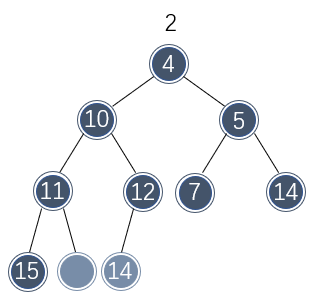
这样空缺处逐渐移动到了树叶位置,此时可以将最后位置的值移动到空缺处了:
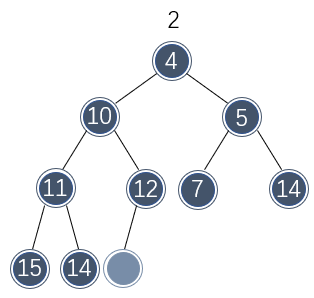
整个删除过程完毕。这种删除策略称为下沉或向下渗透(percolate down)。它的原理并不会比插入复杂多少,不过考虑的细节较多。以下展示了删除的代码实现:
删除过程中需要考虑一个节点可能未必都会有两个子节点,还可能出现只有一个子节点的情况。不过如果只存在一个子节点,那么此时已经到达了数组的结尾。
接下来分析二叉堆操作的时间复杂度。从直观上看,如果插入过程中待插入元素很小,那么需要花费 \\( O(\log N) \\) 的时间才完成插入;但问题是待插入元素未必很小,它应该被插入的层级也应该是 \\( O(\log N) \\) 的增长规律,因此插入的时间复杂度为 \\( O(1) \\) 。
这里进一步解释插入的时间复杂度为什么是常数级。如果将一个元素从底层插入堆中,因为每层包含的元素都是上一层的两倍,它应该有 \\( 1/2 \\) 的概率插入到最底层,此时节点不需要移动;还有 \\( 1/2^2 \\) 的概率插入到次底层,此时路径上的节点需要向下移动 1 层;并且有 \\( 1/2^3 \\) 的概率插入到再次底层,此时路径上的节点需要向下移动 2 层,以此类推。
将这些动作的耗时按概率加起来就是总的复杂度:
\\[ \begin{aligned} T(N) &= 0 \cdot 1/2 + 1 \cdot 1/4 + 2 \cdot 1/8 + \cdots\\ &= 1 \\ &= O(1) \end{aligned} \\]
因此,如果将 \\( N \\) 个元素使用插入的方式创建一个二叉堆,其时间复杂度将为 \\( O(N) \\) 。
在删除时,去除的最小值位于二叉堆的根部,而树叶处的一个元素需要被移动,这使得基本上从树根到树叶这一路径上的每一个元素都需要被移动,因此其时间复杂度为 \\( O(\log N) \\) 。
d-堆
二叉堆的左/右子节点不像二叉查找树一样具有明确的含义,因此子节点的个数不必局限于两个。d-堆是对二叉堆的一个简单的推广,每个节点都有 d 个子节点。
下图展示了一个 3-堆的结构:
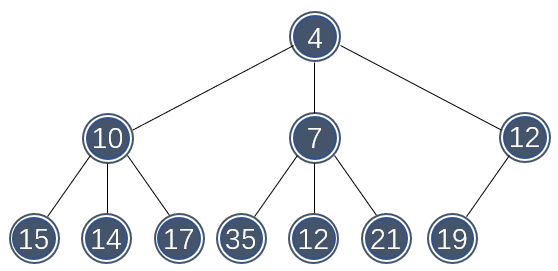
二叉堆实质就是一个 2-堆。d-堆的深度随着 d 的增大而快速减小,插入操作的时间为 \\( O(\log_d N) \\) 。
不过在删除时,由于子节点变多了,要从中找出最小值也需要更多时间,使得删除的时间复杂度为 \\( O(d \log_d N) \\) 。除此之外,如果 d 不为 2 ,节点对应的索引值的计算也更加复杂一些。因此,d 值应该谨慎选择。
左式堆
左式堆的概念
将两个堆合并是一种比较复杂的操作。如果要对两个二叉堆做合并,最简单的操作就是遍历二叉堆,并将每个元素插入到另一个二叉堆中。然而,遍历需要花费 \\( O(N) \\) 的时间,这在堆较大时效率并不高。
左式堆(leftist heap)是另一种优先队列的实现,它除了支持堆序性质和优先队列需要的操作外,还提供了一种更快速的合并操作。
如果要实现比线性级更快的插入操作,那么便需要使用指针,因为调整一次指针能够影响堆的一部分而不仅是单一元素。因此左式堆像传统的二叉树一样使用类似链表一样的思路来管理树,但是处理指针肯定比处理索引更复杂,这会使左式堆在一般的操作下会花费同一量级的稍多时间。
左式堆也是一棵二叉树,不过它趋于非常不平衡。要了解左式堆的性质,需要知道零路径长的定义。节点的零路径长(null path length, NPL)指的是一个节点到一个不全有两个子节点的节点的最短路径的长,记为 \\( Npl(X) \\) 。
显然,不全有两个子节点的节点的 \\( Npl \\) 为 0 ,任一节点的 \\( Npl \\) 比它两个子节点的零路径长的最小值多 1 。根据该结论,可以认为 \\( Npl(NULL) = -1 \\) 。
左式堆的特点为:对堆中的每一个节点,左子节点的 \\( Npl \\) 不比右子节点的 \\( Npl \\) 小。因此一个左式堆的任意子堆还是左式堆。
使用如下方式定义左式堆:
下图展示了一棵合理的左式堆,每个节点的 \\( Npl \\) 标注在节点内:
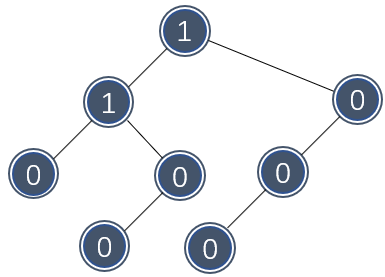
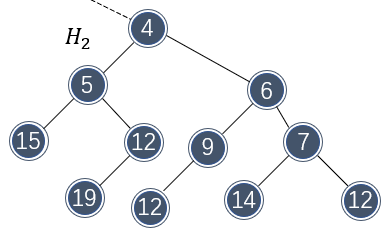
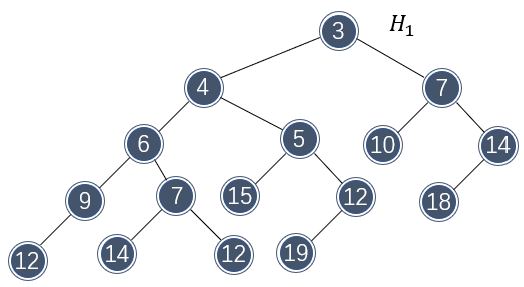
由此可见,左式堆很不平衡,总有向左生长的特性。左式堆的元素排布和二叉堆一样,都是上小下大。接下来看看这些特性是如何使左式堆可以快速合并的。假设需要合并如下两个左式堆:
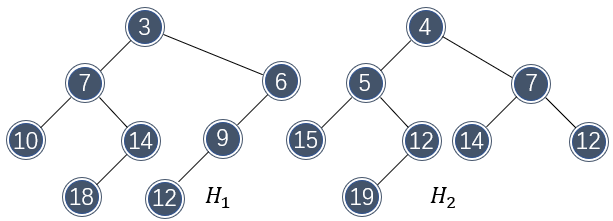
那么首先需要比较两个堆树根的大小,以确定哪个根将作为新根。由于 \\( H_1 \\) 的根部更小,因此将 \\( H_2 \\) 和 \\( H_1 \\) 的右子树做合并:
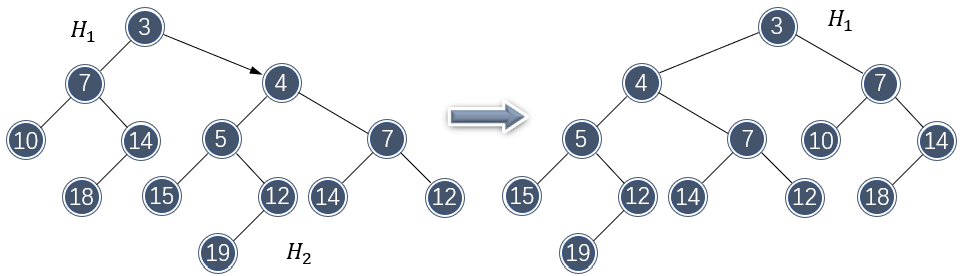
注意到合并破坏了左式堆的性质。不过由于 \\( H_2 \\) 和 \\( H_1 \\) 的左子树保持左式堆不变,只需要将 \\( H_1 \\) 的两个子节点做交换即可重新变为左式堆。
以上合并还没有完成,因为 \\( H_1 \\) 的右子树还没有合并进去,还需要将这一部分与 \\( H_2 \\) 做合并:
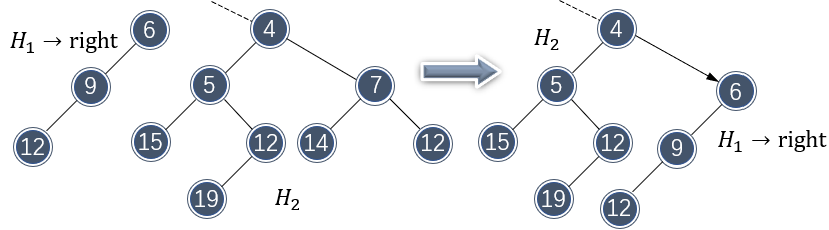
合并仍然是朝右子树方向。同样地,接下来还需要对 \\( H_2 \\) 的右子树做合并:
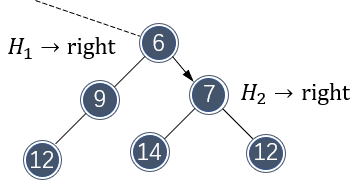
不过,合并破坏了 \\( H_2 \\) 的左式堆性质,需要交换子节点元素做调整:
调整完成后,总体看一下 \\( H_1 \\) ,两个左式堆确实完美地合并了:
左式堆的合并代码比较难以编写,因为各种循环需要考虑的条件有点多。使用递归是一种比较简洁的实现方式。首先需要一个入口函数,判断两个堆的合成主被动关系:
如果需要将 \\( H_2 \\) 合并到 \\( H_1 \\) ,首先需要检查 \\( H_1 \\) 的左侧是否有元素;如果有,那么可以立即插入左侧位置,无需额外调整;否则,将右侧的节点递归地与 \\( H_2 \\) 合并,然后根据节点的 \\( Npl \\) 判断左式堆的性质是否发生了改变,适当做一些调整。
合并的实际代码实现如下:
注意,两个函数间相互调用,由此形式一种递归的关系。
之所以合并时需要朝着右侧节点的方向执行,是因为左式堆具有向左生长的特性,因此右侧节点的长度不会超过节点的期望深度 \\( \log N \\) ,因此合并的时间复杂度也为 \\( O(\log N) \\) ,这也就是左式堆的思想。
既然左式堆往往被用作优先队列,那么它需要具备优先队列的操作:插入和删除最小值。之所以先介绍左式堆的合并操作,是因为插入和删除最小值都可以使用合并来描述。
例如,插入可以视为一棵只有树根的树与一个左式堆合并:
那么插入的时间复杂度也为 \\( O(\log N) \\) 。这也是左式堆的一个弊端:为了实现较快的合并,它不得不牺牲插入的速度。
左式堆的删除可以通过去除树根元素后,将其左右子节点合并成一个新堆实现:
此过程的时间复杂度也为 \\( O(\log N) \\) 。
优先队列作为一种比较实用的数据类型,在许多队列的改进应用场景都能看到。本节介绍优先队列,主要是为下一节介绍排序算法做基础,堆与一种特别的排序算法“堆排序”密切相关。