数据结构03-栈和队列

数据结构与算法 2022年8月4日

很多时候都需要将表作为某个暂时存储的容器，此时就需要频繁地添加或删除表中的元素。

然而，线性表的插入或删除需要线性时间，显然不适合频繁修改。链表的修改虽然需要只需要常数级时间，但是涉及内存的动态分配、指针的调整等，操作还是有些复杂。

本节介绍栈和队列的概念，栈和队列可以看作特殊的线性表，它们主要简化了插入或删除的操作，使得这一过程非常高效，很适合用于密集的调整操作。

栈

栈的概念

栈(stack)是限制插入和删除都只能在一个位置上进行的表，该位置是表的末端，又称为栈顶(top)。下图列出了栈的概念：

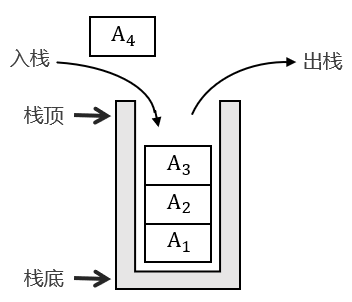
对栈的基本操作有入栈(push)和出栈(pop)，前者向栈内添加一个元素，后者向栈内移除一个元素。从图中可以看出，栈的特点是后添加的元素必须先被移除后，才能处理前面添加的元素，因此栈有时又被称为后进先出(last in first out, LIFO)表。

栈需要有一个栈顶指针实时指示栈顶的位置，对栈元素的访问及修改等操作都通过栈顶指针来实现。当元素入栈或出栈时，栈顶指针也相应被改变。一般来说，栈顶指针不能轻易被改变，因此栈顶指针指向的元素是唯一的可见元素。

栈可以使用许多形式实现，首先来看最简单的数组实现方式。

栈的数组实现

数组实现避免了直接使用指针，是更加简单且应用广泛的解决方案。这种方式的唯一缺点是需要提前声明一个数组的大小。

用数组实现下，每一个栈结构需要有一个成员 topptr ，用于指示栈顶在数组中的哪一个位置。对于空栈而言，它的值一般是是 -1 或 0 。下图展示了栈的数组实现模型：

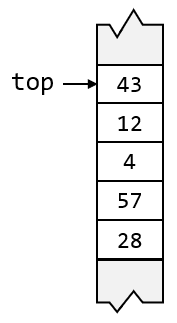
根据以上介绍，栈的数组实现的结构定义为：

typedef struct {
    int size;
    int topptr;
    elemtype* body;
} stack;

#define STACK_NULLTOP (0)

数组实现下，栈的入栈和出栈操作分别如下：

为了将某个元素压入栈中，需要将栈顶位置上移一层，然后置栈的栈顶位置为入栈元素。相应的实现为：

bool Stack_IsFull(stack* s) {
    return s->topptr >= s->size - 1;
}
status Stack_Push(elemtype value, stack* s) {
    if (Stack_IsFull(s))
        return 1;  // stack full
    s->body[++s->topptr] = value;
    return 0;
}

由于数组的容量总是有限的，因此需要先判断栈是否已满。如果在栈已满的情况下继续入栈，将不可避免地发生栈顶越界，可能会与其余部分的数据发生冲突。因此对栈应该小心操作。

为了弹出栈元素，直接让栈顶位置下移一层即可：

bool Stack_IsEmpty(stack* s) {
    return s->topptr == STACK_NULLTOP;
}
status Stack_Pop(stack* s) {
    if (Stack_IsEmpty(s))
        return 1;  // stack empty
    s->topptr--;
    return 0;
}

同样，为了防止栈顶越界，需要提前判断栈是否为空。

入栈和出栈不仅以常数级别的时间实现，而且以非常快的时间运行。大部分机器上都支持寄存器的自增和自减寻址功能，因此栈顶位置移动一层只需要一条机器指令就能实现，入栈也只需要额外执行一次数组的索引赋值即可。

栈舍弃了查找与遍历等操作，实现了非常高效的修改操作。因此，栈是计算机中一种非常基本的数据结构。在大部分机器上甚至内存就是一个栈，可以使用寄存器对内存做入栈和出栈操作，执行效率非常高。

一个影响栈运行效率的因素在于错误检测。对空栈的出栈和对满栈的入栈都会引起数组越界从而导致程序出错。由于这个原因，在某些外部条件确保不会发生溢出的情况下，或在栈的底层实现中，经常会省略处理条件检测。

出栈是一种很有意思的操作，因为它不涉及数据的改变，只需要调整栈顶指针即可。下一次入栈操作时，该元素就会被覆盖，达到删除效果。因此，清空栈只需要将栈顶指针重新置于栈底即可：

void Stack_Clear(stack* s) {
    s->topptr = STACK_NULLTOP;
}

该操作不需要改动任何元素，可以以常数级，并且是非常快的常数级时间完成。

返回栈顶元素可以通过读取栈在栈顶指针位置的元素实现。出栈操作有时也需要读取弹出的元素，其实现就是读取栈顶和出栈的叠加：

elemtype Stack_PopTop(stack* s) {
    if (!Stack_IsEmpty(s))
        return s->body[s->topptr--];
    /* stack empty */
    return 0;  // return value to avoid warning
}

此过程中可能出现栈空的情况，但无法通过返回值提示栈已空，只能通过控制台提示或强制中断代码的执行。

栈的链表实现

由于栈是一个表，因此任何实现表的方式都能实现栈，链表也不例外。如果不能分配一个合理的数组空间，那么更好的方法还是使用链表来实现栈。

这种栈的实现下，测试栈是否是空栈的方式与测试链表是否为空的实现相同，并且栈几乎没有长度限制，无需判断栈是否已满：

bool Stack_IsEmpty(stack s) {
    return s->next == NULL;
}

入栈和出栈在栈的链表实现下的具体操作分别为：

入栈通过向链表开始端添加新的节点实现：

status Stack_Push(stack s, elemtype value) {
    linkedlist_node* cell = malloc(sizeof(linkedlist_node));
    if (cell == NULL)
        return 1;  // stack (memory) full
    cell->elem = value;
    cell->next = s->next;
    s->next = cell->next;
    return 0;
}

出栈通过移除链表开始端的首个节点实现：

status Stack_Pop(stack s) {
    stack first;
    if (Stack_IsEmpty(s))
        return 1;
    first = s->next;
    s->next = s->next->next;
    free(first);
    return 0;
}

链表实现下，入栈和出栈的操作依赖于内存的重新分配，不仅速度较慢，在许多机器上需要依赖操作系统的行为，因此链表实现的栈并不能作为计算机的基本数据结构。

链表实现栈的特点是首节点本身不动，且代表栈顶。下图展示了这一思想：

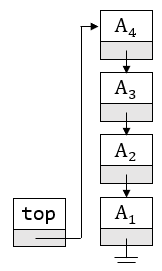
因此，返回栈顶元素通过检查链表的首节点的值实现：

elemtype Stack_Top(stack s) {
    if (!Stack_IsEmpty(s))
        return s->next->elem;
    /* empty stack */
    return 0;  // return to avoid warning
}

链表实现下，出栈后栈的位置无法被重新利用，因此需要显式回收。清空链表的操作需要通过不断执行出栈操作实现，而不能直接修改栈顶指针：

status Stack_Clear(stack s) {
    if (s == NULL)
        return 1;  // not created
    else
        while (!Stack_IsEmpty(s))
            Stack_Pop(s);
}

该操作需要消耗线性时间。考虑到链表的操作更加复杂，因此使用链表实现栈并不是一种很实用的做法。

队列

队列的概念

栈具有后入先出的特性，这意味着先入栈的元素往往得不到优先处理。该特性在一些倒序处理时很实用，然而在顺序处理元素时却无能为力。

通过对栈原理的思考，可以做一些修改而得到队列的概念。类似于栈，队列(queue)也是一个表。然而，队列的插入操作在一端进行，而删除操作在另一端进行。因此队列是先入先出(first in first out, FIFO)的，在保持栈的优点下可以顺序处理元素。

队列的基本操作是入队(enqueue)和出队(dequeue)。入队是在表的末端，即队尾(rear)处插入一个元素；而出队则删除表的第一个元素，即队首(front)处的元素。

下图展示了一个队列的模型：

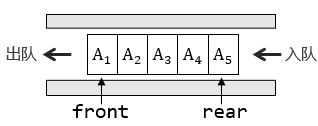
同样地，队列可以由数组或链表实现。不过数组的实现较为常用，因此这里只介绍队列的数组模型。

队列的实现

下图展示了数组模型下，处于中间状态的一个队列：

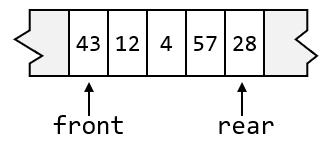
队列两端的元素有着不确定的值。特别地，队列前面的元素曾经属于该队列。

采用以下结构定义实现队列：

typedef struct {
    int size;
    int front;
    int rear;
    int length;
    elemtype* body;
} queue;

这里需要一个成员 length 来记录实际存在队列中的元素个数。

通过队列的类型声明，测试一个队列为空或已满的方法是很容易的：

bool Queue_IsEmpty(queue* q) {
    return q->length == 0;
}
bool Queue_IsFull(queue* q) {
    return q->length == q->size;
}

队列的操作细节和栈比较相似。为了使一个元素入队，让队尾后移，并将元素放入队尾后更新队列长度。

为了使一个元素出队，置队首元素为返回值，然后让队首后移并更新长度。

这种实现的问题在于入队和出队时队列会不断后移（而不是像栈一样栈顶在上上下下的过程中达到平衡），造成队列空间一直向后压缩。当多次入队后，队尾到达的数组的边界，那么下一次入队就会发生队列溢出。

一种简单的解决方法可以参考循环链表的思想，即只要队首或队尾到达数组尾端，它就绕回数组开头，形成循环结构。其实现为：

static int Queue_Succ(queue* q, int pos) {
    if (++pos == q->size)
        pos = 0;
    return pos;
}

如果 front 或 rear 增 1 使得超越了数组，那么其值重置为数组的第一个位置，否则可以放心增 1 。实现绕回并不需要多少附加代码，不过它会使开销变大。如果能保证入队的次数不会大于队列长度，那么没必要使用回绕。

关于队列的循环实现，还需要注意：

  • 检测队列为空或为满非常重要，因为在循环实现下虽然不会发生数组溢出，但是当队首和队尾相邻时，队列自身可能发生交叉，致使自身被自身覆盖
  • 队首和队尾可能有多种表示方法，例如当队列为空时，队首和队尾可能在同一个单元，也可能在相邻单元，这两种情况下队列的长度计算方式不同

这里采用后一种实现，即队首和队尾在相邻单元。和栈一样，为了清空队列，只需要将位置 front 和 rear 修改到合适的位置，并将队列大小置 0 即可，并不需要对队列中的元素作任何改动：

void Queue_Clear(queue* q) {
    q->length = 0;
    q->front = 0;
    q->rear = 1;
}

该操作也可用于初始化队列。

根据以上对队列操作的介绍，入队和出队的操作分为为：

入队：让队尾在逻辑上后移，并将元素放入队尾后更新队列长度，代码实现为：

status Queue_Enqueue(queue* q, elemtype value) {
    if (Queue_IsFull(q))
        return 1;  // queue full
    q->length++;
    q->rear = Queue_Succ(q, q->rear);
    q->body[q->rear] = value;
}

这里的后移是一种逻辑上的后移，因为队列底层是由循环数组支持的，其位置的改变由相应的函数决定。

出队的操作为，置队首元素为返回值，然后让队首后移并更新长度。一般情况下都需要对出队元素做一定处理，否则栈就够用了：

elemtype Queue_Dequeue(queue* q) {
    int elem;
    if (Queue_IsEmpty(q)) {
        /* queue empty */
        return 0;  // return to avoid warning
    }
    q->length--;
    elem = q->body[q->front];
    q->front = Queue_Succ(q->front, q);
    return elem;
}

循环实现下，队列可以在无需移动元素的基础上，不断操作队列两端的元素，使得插入和删除都有着常数级且很快的效率。但也正因如此，队列的维护不像栈那么简单，无法得到计算机底层的直接支持。

队列相比栈，更适合用于处理生活问题。因为在生活情景下，许多问题都需要优先处理先到达的项，并且在处理时随时可能有新的项到达。

近期文章

归档

京ICP备2021034974号
contact me by hello@frozencandles.fun