什么是递归
如果一个函数在执行时,调用了它自身,那么这个函数就会执行自身,然后执行自身时又执行了自身。这种一层一层地向下执行下去的过程称为递归(recursion)。
也就是说,递归的特征为:
...
func(...) # call itself
...
既然递归会一直执行下去,那么必须要在合适的时候让它停止。结束递归是使用递归的难点,因为如果递归代码中没有终止递归的条件测试部分,一个调用自己的函数会无限递归。要终止一个循环只需要使用 break 语句;而要终止一个递归也很简单,只需要让函数不再调用自身即可。
既然在递归时,有时候允许继续递归,有时候需要终止递归,那么肯定要在函数调用前给它一个信号。这个信号一般是用过参数的传递来作用的,因此在递归调用时,需要注意如何给调用的函数设计传入的参数,以及如何根据传入的参数中断递归。
下面根据一个具体的示例来介绍递归的原理:
以上调用一个可以发生递归的函数,结果为:
在代码中调用了 up_and_down() 函数,这次调用称为“第 1 级递归”。然后 up_and_down() 调用自身,这次调用称为“第 2 级递归”。接着第 2 级递归调用第 3 级递归,以此类推。该示例程序共有 3 级递归。程序通过显示变量 n 的值,演示了执行的语句及变量的值。
首先,程序调用了带参数 1 的 up_and_down() 函数,该函数先在 #1 处打印 floor 1 。然后,由于 n 小于 3 ,该函数调用实际参数为 n + 1(即 2 )的 up_and_down() 函数,再在 #1 处打印 floor 2 。与此类似,接下来打印的是 floor 3 。当执行到第 3 级时,n 的值是 3 ,所以 if 测试条件为假。up_and_down() 函数不再调用自己。第 3 级调用接着执行打印语句 #2 ,即打印 floor 3 。此时,第 3 级调用结束,控制被传回它的主调函数,即第 2 级调用,接着执行 if 语句后,即 #2 处打印 floor 2 ,然后第 2 级调用结束,控制被传回第 1 级调用,以此类推。下图展示了这一过程:
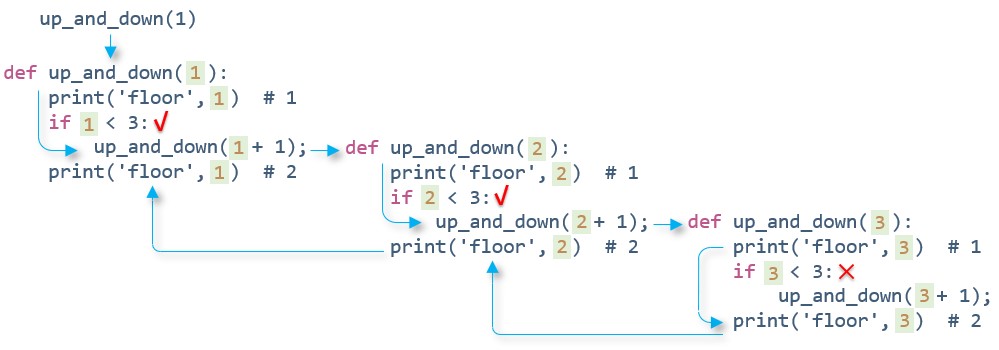
注意,每级递归的变量 n 都属于本级递归私有,这点从程序输出的变量值可以看出。因此每次调用函数时的局部变量都是互不相关的。虽然每级递归都有自己的变量,但是并没有拷贝函数的代码。程序按顺序执行函数中的代码,而递归调用就相当于又从头开始执行函数的代码。
递归调用尤其要注意语句执行的顺序。递归函数中位于递归调用之前的语句,均按被调函数的顺序执行。因此,以上程序在 #1 处按顺序打印 1 2 3 。递归函数中位于递归调用之后的语句,均按被调函数相反的顺序执行。因此,以上程序在 #2 处打印 3 2 1 。
递归调用的这种特性在解决涉及相反顺序的编程问题时很有用。稍后将介绍一个这样的例子。
除了为每次递归调用创建变量外,递归调用非常类似于一个循环语句。递归比循环更直观、容易理解,但是编写出一个合适的递归语句则比较难。除此之外,递归会产生空间上的额外开销,这点放到后面详细介绍。
递归的用法
编写合适的递归函数
要编写合适的递归语句,也需要像编写循环一样,考虑以下两个问题:
- 递归过程中,上一级函数与下一级函数的关系
- 什么时候退出递归
例如,如果使用递归的方式计算阶乘,那么根据阶乘的定义:
而 \\( (n-1)! \\) 则表示为 \\( (n-1)! = (n-1) \cdots 3 \cdot 2 \cdot 1 \\) ,那么由此可得上一级函数与下一级函数的关系为:\\( (n)! = n \times (n-1)! \\)
还需要注意的是阶乘的终止条件,根据阶乘的定义,阶乘的终止条件就是乘到 1 后,有 \\( 1!=1 \\) 。因此,阶乘也可以定义为:
以下将其翻译成了代码语句:
以上是一个很简单的示例,接下来再看一个更复杂的示例:使用递归实现二分查找法。
二分查找法是一种在有序序列中查找某一特定元素的查找算法,其过程如下:首先检查序列的中间元素,如果中间元素正好是待查找的元素,则结束查找;如果待查找的元素大于或者小于中间元素,则在序列大于或小于中间元素的那一半中使用相同方式查找。除此之外,找到最后发现剩下的一半序列为空,则说明待查找的元素不存在。
二分查找法每一次递归都使查找范围缩小一半,因此特别适合在很大的序列中查找一个元素。不过二分查找法有一个前提就是序列必须是有序的。
以上递归的要点都已经在背景资料里着重标出。根据递归的原理,相应的二分查找函数如下:
具体的细节就不再重复介绍。可以自行比对背景介绍了解每一条语句的由来。
递归和倒序计算
递归在处理倒序时非常方便。在解决这类问题中,递归比循环简单,因为循环还需要对结果做反序操作。
以下使用递归来将十进制数转换为二进制数。在给出函数前,先介绍该转换算法的原理。
在二进制中,对于数字 \\( n \\) ,其二进制的最后一位是 \\( n \text{mod} 2 \\) 。因此,计算的第一位数字实际上是待输出二进制数的最后一位。
要获得下一位数字,必须把原数除以 2 。这种计算方法相当于在十进制下把小数点左移一位,然后再计算新的 \\( n \text{mod} 2 \\) ,这样得到的就是待输出二进制数的倒数第二位。通过重复这个过程,便可以得到十进制数等价的二进制。
程序停止计算的依据是当与 2 相除的结果小于 2 ,因为只要结果大于或等于 2 ,就说明还有二进制位。每次除以 2 就相当于去掉一位二进制,直到计算出最后一位为止。
以下程序演示了上述算法:
检查一下编写的函数是否正确:
使用系统自带的计算器验算,可以看到结果完全正确:

如果不用递归,由于这种算法要首先计算最后一位二进制数,所以在显示结果之前必须把所有的位数都储存起来。
递归的缺点
递归既有优点也有缺点。优点是递归为某些编程问题提供了最简单的解决方案。缺点是一些递归算法会快速消耗计算机的内存资源。另外,递归函数不方便维护。
以下函数用递归计算斐波那契数列的值,它接受正整数 n ,返回该项对应的数值。根据斐波那契数列的定义,如果 n 是 1 或 2 ,fibonacci(n) 应返回 1 ;对于其他数值,则应返回 fibonacci(n-1) + fibonacci(n-2) 。它很符合递归的条件,因此,函数可以是:
该函数使用了双递归,即函数每一级递归都要调用本身两次。这产生了一个问题:假设 n 足够大,在第 1 级递归调用,将创建一个变量 n ,然后在该函数中要调用自身两次;在第 2 级递归中要分别创建 2 个变量 n ,这 2 次调用中的每次调用又会发生 2 次调用,因而在第 3 级递归中要创建 4 个名为 n 的变量。此时总共创建了 7 个变量。由于每级递归创建的变量都是上一级递归的 2 倍,所以变量的数量呈指数增长,这很快就会产生非常大的内存,消耗掉计算机的大量内存,很可能导致程序崩溃。
尾递归
如果把递归调用置于函数的末尾,即正好在 return 语句之前,这种形式的递归被称为尾递归(tail recursion)。以上编写的很多递归函数都是尾递归,尽管递归语句可能并不放在函数的最后一行。
尾递归是最简单的递归形式,因为它在某种程度上可以表达为循环。除此之外,尾递归一个很大的特点是它可以被优化。
递归的另一个问题在于每一次调用函数,都需要存储局部变量和参数,这会产生一定的内存开销。但是在递归发生时,函数调用并没有结束,因而这一部分内存并没有被释放,还在内存中存在,因此很深的递归会导致大量内存被占用。
熟悉别的编程语言的读者可能会明白函数是使用栈传递参数的,Python 也不例外,不过这里不具体展开说明。
尾递归的特殊性在于发生递归调用时,函数已经执行到最后了,因此局部变量和参数已经不再需要,这部分内容占据的空间完全可以忽略。
例如,以上的阶乘函数:
注意,尽管很像,但是该递归并不是尾递归,因为在发送递归时,局部变量 n 的值还没有被利用。如果把 factorial(5) 递归展开,那么它会变成如下形式:
(5 * factorial(4)) =>
(5 * (4 * factorial(3)))) =>
... =>
(5 * (4 * (3 * (2 * (1 * 1))))))
由此可见,递归过程中产生的中间变量只有在递归结束后才会被一起利用,这就产生了大量的空间上的浪费。
如果把以上阶乘函数改成尾递归形式,变成:
这就是真正的尾递归,它的调用会变成:
factorial(4, 5) =>
factorial(3, 20) =>
factorial(2, 60) =>
factorial(1, 120) =>
120
这一过程中,每次的调用不再需要用到上一次调用的变量了,因此这部分中间变量完全可以抛弃。在一些语言中,尾递归会在编译阶段被编译器通过优化转换成循环语句。
但是很遗憾,Python 并没有优化递归的功能,并且 Python 对嵌套递归的深度也有限制,递归深度上限默认为 1000 ,或者可以通过 sys.setrecursionlimit() 函数修改这个值。不过尾递归在编写代码时,完全可以使用循环代替,这就是手动形式的优化了。
总的来说,递归不仅占用内存更多,并且由于每次函数调用要花费一定的时间,递归的执行速度也更慢,因此简单的递归应该使用循环代替。但递归较循环语句更简洁,而且在某些情况下,不能用简单的循环代替递归。
参考资料
本文的许多思路都来自于对《C Primer Plus》相关章节的读书笔记。