插值的概念
插值(interpolate)就是将一组离散的点用一条曲线连接起来的过程。插值计算一般可能用在如下的场景中:其一是数据扩充,插值可以利用现有数据加工出新的类似数据,有时也可用于近似计算;其二是数据压缩,如果指定了插值方式,那么只需要存储少数点就可以还原曲线。
如果对一系列点 \\( (x_1,y_1),(x_2,y_2),\dots,(x_n,y_n) \\) ,能找出一个函数 \\( y=P(x) \\) ,使得对于任意点 \\( (x_i,y_i) \\) 有 \\( P(x_i) = y_i\ \\) ,那么就称函数 \\( y=P(x) \\) 插值了这些点。
插值函数有很多种,例如最常用的多项式函数、有理分式函数,或者三角函数等,还可以是分段函数。多项式常常用于插值,因为多项式在各种计算中都十分方便。本节介绍最基本的多项式插值的方法。
插值方法
插值方法就是求插值函数 \\( f(x) \\) 的方法。这里介绍两个最常用的求多项式插值函数的方法:拉格朗日插值法和牛顿插值法。
拉格朗日插值法
拉格朗日插值法很简单。对一系列点 \\( (x_1,y_1),(x_2,y_2),\dots,(x_n,y_n) \\) ,可以用以下 \\( n-1 \\) 次多项式表达它:
\\[
\begin{align}
P_{n-1}(x) &= y_1L_1(x) + y_2L_2(x) + \dots + y_nL_n(x) \\
\text{where} \quad L_k(x) &= \frac{(x-x_1)\cdots(x-x_{k-1})(x-x_{k+1})\cdots(x-x_n)}{(x_k-x_1)\cdots(x_k-x_{k-1})(x_k-x_{k+1})\cdots(x_k-x_n)} \\
&= \prod_{\substack{0\lt i \lt n \\ i \neq k}} \frac {x-x_i}{x_k-x_i}
\end{align}
\\]
这个函数可能看着有些抽象,如果写的具体点,例如通过 3 个点的二次函数的表达式为:
\\[
P_2(x) = \frac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)} y_1 + \frac{(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)} y_2 + \frac{(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)} y_3
\\]
每一项前的分式都具有一个有趣的性质:例如第一项的 \\( \dfrac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)} \\) ,当 \\( x\neq x_1 \\) 时,不论它是 \\( x_2 \\) 还是 \\( x_3 \\) ,这一项都为 0 ,而当 \\( x = x_1 \\) 时,分子分母相等从而相消变成了 1 ,这样有 \\( L_k(x_k) = 1 \\) ,而 \\( j\neq k \\) 时 \\( L_k(x_j) = 0 \\) ,从而使
\\[
\begin{align}
P_{n-1}(x_k) &= 0 + 0 + \dots + y_k L_k(x_k) + 0 + \dots + 0 = y_k \\
&= y_k
\end{align}
\\]
满足插值要求。
拉格朗日插值法得到的是有效的插值多项式,也是满足点 \\( (x_1,y_1),(x_2,y_2),\dots,(x_n,y_n) \\) 的唯一的 \\( n-1 \\) 次或更低次多项式。
证明方法可以采用反证法,假设存在两个这样的至多 \\( n-1 \\) 次多项式 \\( P(x) \\) 和 \\( Q(x) \\) 经过这些点,即 \\( P(x_1)=Q(x_1)=y_1, P(x_2)=Q(x_2)=y_2,\dots,P(x_n)=Q(x_n)=y_n \\) ,相减得到一个新的多项式 \\( R(x) = P(x)-Q(x) \\) ,\\( H(x) \\) 最多也是 \\( n-1 \\) 次,并且对于 \\( n \\) 个点 \\( x_1,x_2,\dots,x_n \\) ,它们都是 \\( H(x) \\) 的零点。但根据代数学基本定理,一个 \\( n-1 \\) 次的多项式最多只有 \\( n-1 \\) 个零点,除非它是值恒为 0 的常数多项式。这样,\\( P(x)=Q(x) \\) ,说明多项式是唯一的。
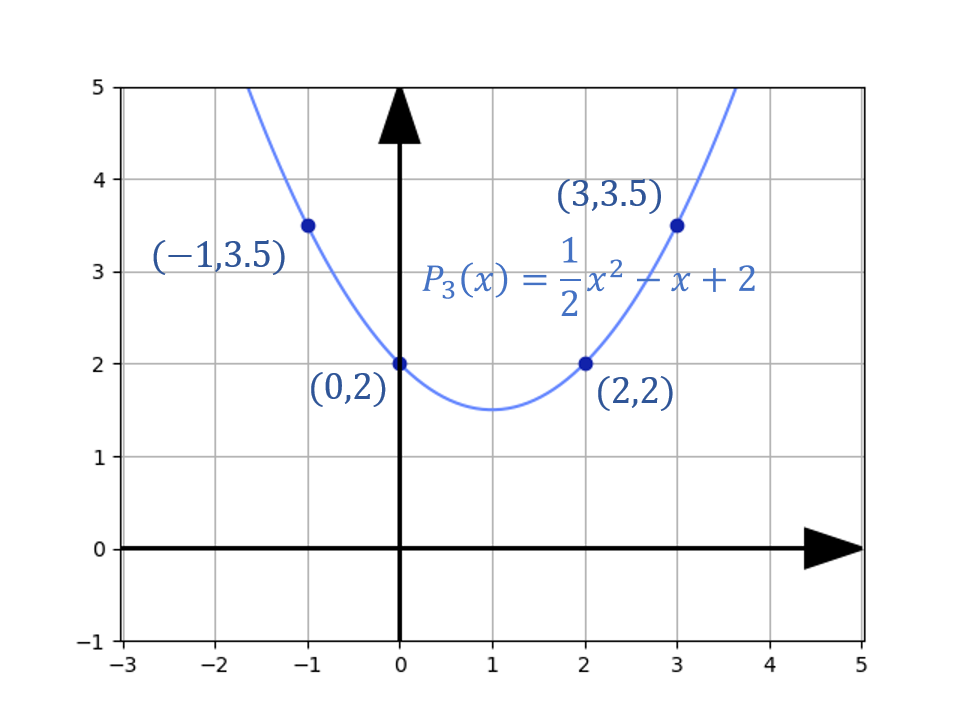
例如,对 \\( (-1, 3.5), (0, 2), (2, 2), (3, 3.5) \\) 这些点应用拉格朗日插值的过程为:
\\[
\begin{array}{lll}
P_3(x) &=& 3.5 \dfrac {(x-0)(x-2)(x-3)}{(-1-0)(-1-2)(-1-3)} + 2 \dfrac {(x-(-1))(x-2)(x-3)}{(0-(-1))(0-2)(0-3)} \\
& & + 2 \dfrac {(x-(-1))(x-0)(x-3)}{(2-(-1))(2-0)(2-3)} + 3.5 \dfrac {(x-(-1))(x-0)(x-2)}{(3-(-1))(3-0)(3-2)} \\
&=& -\dfrac 7 {24} (x^3-5x^2+6x) - \dfrac 1 3 (x^3-2x^2-3x) \\
& & + \dfrac 1 3 (x^3-4x^2+x+6) + \dfrac 7 {24} (x^3-x^2-2x) \\
&=& \dfrac 1 2 x^2 - x + 2
\end{array}
\\]
这个函数不仅经过点 \\( (-1, 3.5), (0, 2), (2, 2), (3, 3.5) \\) ,同时也是经过这几个点的唯一一个 2 次函数,如下所示:
牛顿插值法
拉格朗日插值法直观且易于理解,但它的缺点是当插值节点的个数增加时,拉格朗日函数需要重新计算,当插值节点数较多时计算量非常大,在实际使用中很不方便。牛顿插值法是一种在增加节点时更灵活的插值方法。牛顿插值法在插值多项式增加一个项时,只需要额外计算一项,从而避免大量的无用计算。
任何一个不高于 \\( n \\) 次的多项式,都可以表示成
\\[
\begin{align}
& 1 \\
& x - x_1 \\
& (x - x_1)(x - x_2) \\
& \cdots \\
& (x - x_1)(x - x_2) \cdots (x - x_n)
\end{align}
\\]
的线性组合。也就是说,满足插值条件 \\( P(x_i)=y_i \; (i=1,2,\dots,n) \\) 的 \\( n-1 \\) 次插值多项式,可以表示为:
\\[
P(x) + a_0 + a_1(x - x_0) + a_2(x - x_0)(x - x_1) + \cdots + a_n(x - x_0)(x - x_1) \cdots (x - x_{n-1})
\\]
待定系数 \\( a_i \\) 的确定方法如下:考虑当 \\( x=x_0 \\) 时,\\( P(x_0) = a_0 = y_0 \\) ;而当 \\( x=x_1 \\) 时,\\( P(x_1) = a_0 + a_1(x-x_0) = y_1 \\) ,那么就可以推出 \\( a_1 = \cfrac{y_1-y_0}{x_1-x_0} \\) ,这项系数称为一阶均差或一阶差商。
当 \\( x=x_2 \\) 时,\\( P(x_2)=a_0+a_1(x_2-x_0)+a_2(x_2-x_0)(x_2-x_1)=y_2 \\) ,可以推出 \\( a_2=\cfrac{\cfrac{y_2-y_0}{x_2-x_0} - \cfrac{y_1-y_0}{x_1-x_0}}{x_2-x_1} \\) ,这项系数称为二阶均差或二阶差商。
以此类推便可以得到后面每一项的系数。用 \\( f[x_1,\dots,x_n] \\) 表示由 \\( x_1,\dots,x_n \\) 确定的(唯一)多项式的 \\( x^{n-1} \\) 项的系数,那么具有如下递推关系:
\\[
\begin{align}
f[x_k] &= y_k \\
f[x_k,x_{k+1}] &= \frac{f[x_{k+1}]-f[x_k]}{x_{k+1}-x_k} \\
f[x_k,x_{k+1},x_{k+2}] &= \frac{f[x_{k+1},x_{k+2}]-f[x_k,x_{k+1}]}{x_{k+2}-x_k} \\
f[x_k,x_{k+1},x_{k+2},x_{k+3}] &= \frac{f[x_{k+1},x_{k+2},x_{k+3}]-f[x_k,x_{k+1},x_{k+2}]}{x_{k+3}-x_k} \\
\end{align}
\\]
牛顿差商的递归定义可以组织为一个方便使用的表,称为差商表,形式如下
\\[
\begin{array}{cccccc}
x_1 & \color{red}{f[x_1]} \\
x_2 & f[x_2] & \color{red}{f[x_1,x_2]} \\
x_3 & f[x_3] & f[x_2,x_3] & \color{red}{f[x_1,x_2,x_3]} \\
x_4 & f[x_4] & f[x_3,x_4] & f[x_2,x_3,x_4] & \color{red}{f[x_1,x_2,x_3,x_4]} \\
\cdots & \cdots & \cdots & \cdots & \cdots & \color{red}{\cdots} \\
x_n & f[x_n] & f[x_{n-1},x_n] & f[x_{n-2},x_{n-1},x_n] & f[x_{n-3},x_{n-2},x_{n-1},x_n] & \cdots & \color{red}{f[x_1,x_2,\dots,x_n]} \\
\end{array}
\\]
主对角线上的差商即为所求的待定系数 \\( a_i \\) ,代入函数中展开即得所求插值多项式。
例如,使用差商表找出经过三个点 \\( (0,1),(2,2),(3,4) \\) 的插值多项式过程如下:
\\[
\begin{array}{l|lll}
0 & \color{red}{f[x_1]=1} \\
2 & f[x_2]=2 & \color{red}{f[x_1,x_2]=\dfrac{f[x_2]-f[x_1]}{x_2-x_1}=\dfrac{2-1}{2-0}=\dfrac 1 2} \\
3 & f[x_3]=4 & f[x_2,x_3]=\dfrac{f[x_3]-f[x_2]}{x_3-x_2}=\dfrac{4-2}{3-2}=2 &
\color{red}{f[x_1,x_2,x_3]=\cfrac{f[x_2,x_3]-f[x_1,x_2]}{x_3-x_1}=\cfrac{2 - \cfrac 1 2}{3-0}=\dfrac 1 2} \\
\end{array}
\\]
多项式系数可以从表的主对角线中得到,为 \\( a_0 = f[x_1], a_1 = f[x_1,x_2], a_2 = f[x_1,x_2,x_3] \\) ,从而插值多项式为:
\\[
\begin{align}
P_2(x) &= 1 + \frac 1 2 (x-0) + \frac 1 2 (x-0)(x-2) \\
&= \frac 1 2 x^2 - \frac 1 2 x + 1
\end{align}
\\]
这个二次插值多项式不仅是唯一的,并且和拉格朗日法计算的结果一致。
如果继续插入第 4 个点 \\( (4,5) \\) ,那么差商表扩充为:
\\[
\begin{array}{c|cccc}
0 & \color{red}{1} \\
2 & 2 & \color{red}{\dfrac 1 2} \\
3 & 4 & 2 & \color{red}{\dfrac 1 2} \\
4 & 5 & \dfrac{f[x_4]-f[x_3]}{x_4-x_3}=1 & \dfrac{f[x_3,x_4]-f[x_2,x_3]}{x_4-x_2}=-\dfrac 1 2 &
\color{red}{\dfrac{f[x_2,x_3,x_4]-f[x_1,x_2,x_3]}{x_4-x_1}=-\dfrac 1 4} \\
\end{array}
\\]
得到新的 3 阶多项式如下:
\\[
\begin{align}
P_3(x) &= 1 + \frac 1 2 (x-0) + \frac 1 2 (x-0)(x-2) - \frac 1 4 (x-0)(x-2)(x-3) \\
&= -\frac 1 4 x^3 + \frac 7 4 x^2 - 2 x + 1
\end{align}
\\]
注意到 \\( P_3(x) = P_2(x) - \dfrac 1 4 (x-0)(x-2)(x-3) \\) ,因此计算新的多项式时,只需要在原有部分添加一项即可,无需全部重新计算。
样条曲线
龙格现象与三次样条
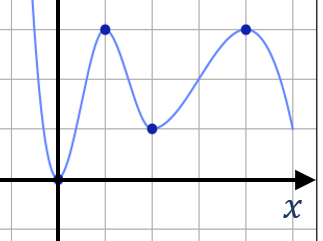
多项式可以对任意数量的点集插值,但是多项式的特性可能会在插值时出现一些问题。如下图所示:
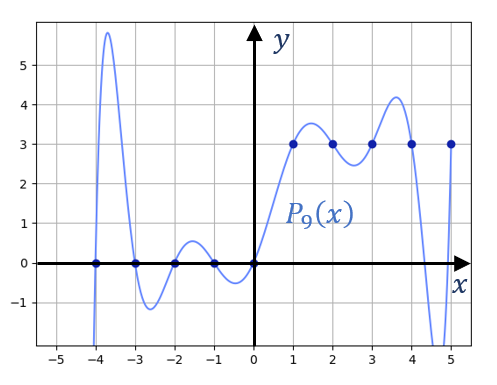
当 \\( |x| \\) 较大时,多项式的最高次项对曲线形状的影响比其它项大得多,因此造成曲线在插值区间两侧的端点处有很大的凸起,这称为龙格现象(Runge phenomenon)。
因此,当插值点数 \\( n>8 \\) 时,一般较少直接使用多项式插值。
样条(spline)是另一种数据插值的方式,它通过分段构成的曲线为数据插值,每段曲线都是低阶多项式。
三次样条(cubic spline)是使用较广泛的样条,之所以使用三次,是因为三次曲线可以使分段点的一阶导数(斜率)和二阶导数(曲率)连续,而更低阶的多项式无法主动调整。三次样条的公式表现如下:
\\[
\begin{align}
S_1(x) &= y_1 + b_1(x-x_1) + c_1(x-x_1)^2 + d_1(x-x_1)^3 \quad x \in [x_1,x_2] \\
S_2(x) &= y_2 + b_1(x-x_2) + c_1(x-x_2)^2 + d_1(x-x_2)^3 \quad x \in [x_2,x_3] \\
&\cdots \cdots \\
S_{n-1}(x) &= y_{n-1} + b_1(x-x_{n-1}) + c_1(x-x_{n-1})^2 + d_1(x-x_{n-1})^3 \quad x \in [x_{n-1},x_n] \\
\end{align}
\\]
显然,这些方程都满足 \\( S_i(x_i)=y_i \\) ,符合插值要求。为了使各个曲线之间可以相接,还要求 \\( S_i(x_{i+1})=y_{i+1} \\) ,其中 \\( i=1, 2, \dots, n-1 \\) 。
此外,为了使曲线间的连接光滑,还要求连接点处一阶导数(斜率)和二阶导数(曲率)连续,即 \\( S'_{i}(x_{i+1})=S'_{i+1}(x_{i+1}) \\) 和 \\( S''_{i}(x_{i+1})=S'_{i+1}(x_{i+1}) \\) ,其中 \\( i=1, 2, \dots, n-2 \\) 。
寻找满足要求的三次样条曲线即求解以上线性方程组。三次样条共有 \\( n-1 \\) 条曲线,每条曲线都需要求解 3 个系数 \\( b_i,c_i,d_i \\) ,因此一共有 \\( 3n-3 \\) 个未知系数。确定相接性质引入了 \\( n-1 \\) 个方程,确定斜率和曲率特性分别引入了 \\( n-2 \\) 个方程,因此一共有 \\( 3n-5 \\) 个未知方程。方程的个数小于未知数的个数,除了某些特定的情况下外,该方程组具有无穷多解,这说明三次样条曲线是不唯一的。
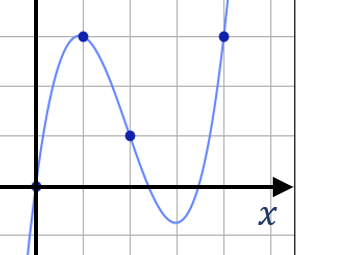
容易验证,对于点 \\( (0,0),(1,3),(2,1),(4,3) \\) ,以下两个都是满足要求的三次样条曲线:
\\[
\begin{align}
S_1(x) &= \frac {29} 4 (x-0) - \frac {41} 8 (x-0)^2 + \frac 7 8 (x-0)^3 \\
S_2(x) &= 3 + \frac 3 8 (x-1) - \frac 5 2 (x-1)^2 + \frac 7 8 (x-1)^3 \\
S_3(x) &= 1 - \frac {11} 4 (x-2) + \frac 1 8 (x-2)^2 + \frac 7 8 (x-2)^3 \\
\end{align}
\\]
\\[
\begin{align}
S_1(x) &= -6 (x-0)^3 - 9 (x-0)^2 \\
S_2(x) &= 4 (x-1)^3 - 6 (x-1)^2 + 3 \\
S_3(x) &= -\frac 1 2 (x-2)^3 + \frac 3 2 (x-2)^2 + 1 \\
\end{align}
\\]
可以通过添加额外的约束条件解决三次样条曲线不唯一的问题。一般来说有如下常见的添加约束方式:
- 额外设定两个端点处的曲率为 0 ,即 \\( S_1''(x_1)=0, S''_{n_1}(x_n)=0 \\) ,这种约束下得到的三次样条称为自然三次样条(natural spline)
- 自定义两个端点处的曲率值 \\( S_1''(x_1), S''_{n_1}(x_n) \\) ,则得到曲率调整三次样条
- 自定义两个端点处的斜率值 \\( S_1'(x_1), S'_{n_1}(x_n) \\) ,则得到钳制三次样条(clamped spline)
- 额外设定前两个和最后两个端点三阶导数分别相等,即 \\( S'''_1(x_2)=S'''_2(x_2), S'''_{n-2}(x_{n-1}=S'''_{n-1}(x_{n-1})) \\) 或 \\( d_1=d_2, d_{n-2} = d_{n-1} \\) ,则得到非纽结三次样条(not-a-knot spline)
- 额外设定两个端点处的函数值、斜率、曲率均相等,即 \\( S_1(x_1) = S_{n-1}(x_n), S'_1(x_1) = S'_{n-1}(x_n), S''(x_1) = S''_{n-1}(x_n) \\) ,则得到三次周期样条(periodic spline)
接下来以三次自然样条为例介绍参数的求解方法。显然,求解参数就是求解线性方程组。引入记号 \\( \Delta x_i = x_{i+1} - x_i \\) 与 \\( \Delta y_i = y_{i+1} - y_{i} \\) ,则曲线方程可以表示为:
\\[
\begin{alignat}{3}
y_2 &= S_1(x_2) &&= y_1 + b_1 \Delta x_1 + c_1\Delta x_1^2 + d_1\Delta x_1^3 \\
& \dots && \dots \tag{0}\\
y_n &= S_{n-1}(x_n) &&= y_{n-1} + b_{n-1} \Delta x_n + c_{n-1} \Delta x_n^2 + d_{n-1} \Delta x_n^3 \\
\end{alignat}
\\]
斜率连续的约束条件可以得到以下方程组:
\\[
\begin{alignat}{3}
0 &= S'_1(x_2) - S'_2(x_2) &&= b_1 + 2 c_1\Delta x_1 + 3 d_1\Delta x_1^2 - b_2 \tag{1}\\
& \dots && \dots \\
0 &= S'_{n-2}(x_{n-1}) - S'_{n-1}(x_{n-1}) &&= b_{n-2} + 2 c_{n-2}\Delta x_{n-2} + 3 d_{n-2}\Delta x_{n-2}^2 - b_{n-1} \\
\end{alignat}
\\]
曲率连续的约束条件可以得到以下方程组:
\\[
\begin{alignat}{3}
0 &= S''_1(x_2) - S''_2(x_2) &&= 2 c_1 + 6 d_1\Delta x_1 - 2 c_2 \\
& \dots && \dots \tag{2}\\
0 &= S''_{n-2}(x_{n-1}) - S''_{n-1}(x_{n-1}) &&= 2 c_{n-2} + 6 d_{n-2}\Delta x_{n-2}^2 - 2 c_{n-1} \\
\end{alignat}
\\]
自然三次样条引入了额外两个约束条件为:
\\[
\begin{align}
S''_1(x_1) = 0 \rightarrow 2c_1 = 0 \\
S''_{n-1}(x_n) = 0 \rightarrow 2c_n = 0 \\
\end{align}
\\]
式 \\( (2) \\) 可用于从 \\( c_i \\) 求解 \\( d_i \\) :
\\[
d_i = \frac {c_{i+1} - c_i}{3\Delta x_i} \quad i = 1, 2, \dots, n-1
\\]
再次代入式 \\( (0) \\) 可继续用于从 \\( c_i \\) 求解 \\( b_i \\) :
\\[
\begin{align}
b_i &= \frac {\Delta y_i}{\Delta x_i} - c_i \Delta x_i - d_i \Delta x_i^2 \\
&= \frac {\Delta y_i}{\Delta x_i} - \frac {\Delta x_i (2c_i + c_{i+1})} 3
\quad i=1, 2, \dots, n-1
\end{align}
\\]
将 \\( b_i \\) 和 \\( d_i \\) 代回式 \\( (1) \\) ,即可表示为只含 \\( c_i \\) 的方程组:
\\[
\Delta x_ic_i + 2(\Delta x_i+\Delta x_{i+1})c_{i+1} + \Delta x_{i+1} c_{i+2} = 3\left( \frac{\Delta y_{i+1}}{\Delta x_{i+1}} - \frac{\Delta y_i}{\Delta x_i} \right) \quad i = 1,2,\dots,n-2
\\]
即求解矩阵方程:
\\[
\begin{bmatrix}
1 & & & & & \\
\Delta x_1 & 2\Delta x_1 + 2\Delta x_2 & \Delta x_2 & \\
& \ddots & \ddots & \ddots & \\
&& \Delta x_{n-2} & 2\Delta x_{n-2} + 2\Delta x_{n-1} & \Delta x_{n-1} \\
&& & & 1 \\
\end{bmatrix} \begin{bmatrix}
c_1 \\
c_2 \\
\vdots \\
\vdots \\
c_{n-1} \\
c_n \\
\end{bmatrix} = \begin{bmatrix}
0 \\
3\left( \dfrac{\Delta y_2}{\Delta x_2} - \dfrac{\Delta y_1}{\Delta x_1} \right) \\
\vdots \\
3\left( \dfrac{\Delta y_{n-1}}{\Delta x_{n-1}} - \dfrac{\Delta y_{n-2}}{\Delta x_{n-2}} \right) \\
0 \\
\end{bmatrix}
\\]
例如,以下矩阵方程用于求解通过 \\( (0,3), (1,-2), (2,1), (3,3) \\) 的自然三次样条:
\\[
\begin{bmatrix}
1 & 0 & 0 & 0 \\
1 & 4 & 1 & 0 \\
0 & 1 & 4 & 1 \\
0 & 0 & 0 & 1 \\
\end{bmatrix} \begin{bmatrix}
c_1 \\
c_2 \\
c_3 \\
c_4 \\
\end{bmatrix} = \begin{bmatrix}
0 \\
24 \\
-3 \\
0 \\
\end{bmatrix}
\\]
解得 \\( \begin{bmatrix} c_1 \\ c_2 \\ c_3 \\ c_4 \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 6.6 \\ -2.4 \\ 0 \\ \end{bmatrix} \\) 。这里的 \\( c_4 \\) 只用于求解其它参数,不参与构成曲线。
得到的 \\( c_i \\) 可以用于求解 \\( d_i \\) 和 \\( b_i \\) :
\\[
\begin{align}
d_1 &= \frac {c_2-c_1}{3\Delta x_1} = 2.2 & b_1 &= \frac {\Delta y_1}{\Delta x_1} - \frac {\Delta x_1 (2c_1 + c_2)} 3 = -7.2 \\
d_2 &= \frac {c_3-c_2}{3\Delta x_2} = -3 & b_2 &= \frac {\Delta y_2}{\Delta x_2} - \frac {\Delta x_2 (2c_2 + c_3)} 3 = -0.6 \\
d_3 &= \frac {c_4-c_3}{3\Delta x_3} = 0.8 & b_3 &= \frac {\Delta y_3}{\Delta x_3} - \frac {\Delta x_3 (2c_3 + c_4)} 3 = 3.6 \\
\end{align}
\\]
所以,以上点构成的自然样条为:
\\[
\begin{align}
S_1(x) &= 3 - 7.2 (x-0) + 2.2 (x-0)^3 \\
S_2(x) &= -2 - 0.6 (x-1) + 6.6 (x-1)^2 - 3 (x-1)^3 \\
S_3(x) &= 1 + 3.6 (x-2) - 2.4 (x-2)^2 + 0.8 (x-2)^3 \\
\end{align}
\\]
贝塞尔样条
贝塞尔样条(Bézier spline)曲线由法国工程师 Pierre Bézier 为雷诺公司生产汽车时所提出。贝塞尔样条由插值点和控制点(control points)组成,控制点并不实际经过,它们负责控制曲线的形状。
目前应用最广泛的是三次贝塞尔样条,三次贝塞尔样条的每一段由 4 个点组成,其中 \\( p_1,p_4 \\) 点是插值点,\\( p_2,p_3 \\) 点是控制点:
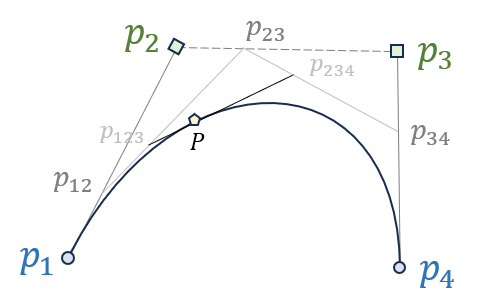
在 \\( t=0 \\) 时刻,辅助点 \\( p_{12} \\) 从 \\( p_1 \\) 出发,匀速前行在 \\( t=1 \\) 时刻到达 \\( p_2 \\) 其余两点 \\( p_{23},p_{34} \\) 类似;同时 \\( p_{123} \\) 从 \\( p_{12} \\) 出发,沿 \\( p_{12},p_{23} \\) 连成的线段前进至 \\( p_{23} \\) ;最后,点 \\( P \\) 也以同样的形式从 \\( p_{123} \\) 到 \\( p_{234} \\) ,\\( P \\) 点经过的路径即为贝塞尔样条。以下小程序有助于理解贝塞尔曲线是如何生成的:
以上绘图动画来自 https://javascript.info/bezier-curve 。这是一个交互式的脚本,读者可以通过拖动修改各个点的位置并观察不同位置时曲线是如何生成的。
贝塞尔样条同时与 \\( p_1p_2 \\) 和 \\( p_3p_4 \\) 相切。以上贝塞尔样条的定义是它的递归定义,类似地很容易定义更高或更低阶的贝塞尔样条。
设插值点 \\( p_1=(x_1,y_1),,p_4=(x_4,y_4) \\) ,控制点 \\( p_2=(x_2,y_2),p_3=(x_3,y_3) \\) ,由定义可得:
\\[
\begin{gather}
p_{12} = p_1 + t (p_2 - p_1) \\
p_{123} = p_{12} + t (p_{23} - p_{12}) = p_1 + (2p_2-2p_1)t + (p_3+p_1-2p_2) t^2 \\
p_{1234} = p_{123} + t (p_{234} - p_{123}) = p_1 + (3p_1 - 3p_2)t + (3p_2 - 6p_2 + 3p_3)t^2 + (p_1 - 3p_2 + 3p_3 - p_4)t^3
\end{gather}
\\]
因此,三次贝塞尔样条就是三次参数方程组成的曲线:
\\[
B(t) = \begin{cases}
x(t) &= x_1 &+ (3x_1 - 3x_2) t &+ (3x_2 - 6x_2 + 3x_3) t^2 &+ (x_1 - 3x_2 + 3x_3 - x_4) t^3 \\
y(t) &= y_1 &+ (3y_1 - 3y_2) t &+ (3y_2 - 6y_2 + 3y_3) t^2 &+ (y_1 - 3y_2 + 3y_3 - y_4) t^3 \\
\end{cases}
\\]
其中 \\( t \in [0,1] \\) 。
三次贝塞尔样条的表达能力非常强,它被广泛应用与计算机中表示矢量曲线,只需要存储较少的点就可以得到很复杂的曲线。例如,以下是 Source Han Serif(思源宋体)字体中表示字母“S”的贝塞尔样条构成: