通用函数
通用函数的概念
numpy 的数组在底层使用了C语言构造存储效率更高,如果对 numpy 的数组使用 Python 的遍历方式,那么效率很低。例如,以下是一个 Python 函数,用于计算数组内每个元素的倒数:
如果对 numpy 的数组调用该函数,计算的速度比较慢:
纯 Python 执行的效率偏低,不过好在 numpy 为数组的各种操作提供了非常方便且高效的接口,这种接口称为通用函数(universal function, ufunc),也称为向量操作。
通用函数使得对数组的简单操作,将会作用于数组的每一个元素。例如,以上倒数的计算可以以运算符“ / ”直接操作数组对象和一个整数,而实际的运算将会发生在数组的每一个元素之间:
通用函数的实际计算由 numpy 底层执行,可以做到 CPU 级别的优化,这样会取得非常快的执行效率:
计算大型数组时,使用通用函数的效率高得多。
使用通用函数
通用函数有一元通用函数和二元通用函数,可以操作一个数组、一个数组和一个数值,甚至两个数组。
numpy 的通用函数重载了 Python 的运算符,因此可以像对一个数值的运算一样对数组内的每个元素做运算。以下是一些示例:
还可以将这些运算符任意组合使用,并且组合使用也遵循运算符的优先级:
所有的运算符都是 numpy 内置函数的简单封装器。例如,运算符“ + ”就是一个 add() 函数的封装:
下表列出了 numpy 重载的运算符与其对应的函数:
| 运算符 | 对应的通用函数 | 描述 |
|---|---|---|
| + | add() | 加法运算 |
| - | subtract() | 减法运算 |
| - | negative() | 负数运算 |
| * | multiply() | 乘法运算 |
| / | divide() | 除法运算,得到的结果是小数 |
| // | floor_divide() | 整数除法运算,得到的结果是向下截断的整数 |
| ** | power() | 指数运算 |
| % | mod() | 模运算(余数运算) |
除了运算符外,numpy 还重载了 Python 内置的运算函数,使这些函数可以应用于数组。
例如,可以使用 abs() 函数取绝对值。当该函数作用于复数数组时,绝对值返回的是该复数在复平面上对应向量的模长:
该重载方法对应的 numpy 通用函数是 absolute() ,并且在 numpy 内还有一个别名也为 abs() 。
numpy 还提供了计算三角函数的通用函数,包括正弦、余弦、正切以及它们对应的反三角函数:
另一类常用的通用函数是指数运算,包括以 e 为底数的指数函数 exp() 、以 2 为底数的指数函数 exp2() 、任意数为底数的指数函数 pow() 。不是特殊的指数运算也可以直接使用指数运算符“ ** ”计算,该运算符对应的通用函数是 power() 。
指数运算的逆运算,即对数运算也是很有用的。最基本的 log() 给出的是以 e 为底数的对数,还有包括以 2 为底数的对数函数 log2() 、以 10 为底数的对数函数 log10() 。
还有一些特殊的函数例如 expm1() 用于计算 ex - 1 ,以及 log1p() 用于计算 ln(x + 1) ,它们在底层做了一定优化,对于非常小的输入值可以保持很好的精度,比间接计算再组合更精确。
通用函数非常灵活,甚至可以对两个数组进行运算:
不仅限于一维函数,也可以用于多维数组的计算:
通用函数与布尔运算
通用函数除了计算外,还有一种实用的用法是布尔运算。这些比较运算符和其对应的通用函数如下表所示:
| 运算符 | 对应的通用函数 |
|---|---|
| == | equal() |
| != | not_equal() |
| < | less() |
| <= | less_equal() |
| > | greater() |
| >= | greater_equal() |
对一个数组对象的布尔运算将对每个元素做布尔运算,并得到一个新的布尔数组:
如果需要对两个布尔结果做布尔逻辑运算,可以通过 Python 的逐位逻辑运算符“ & ”、“ | ”、“ ^ ”和“ ~ ”来实现。当作用与布尔数组时,可以表示布尔逻辑运算:
下表总结了逐位的布尔运算符和其对应的通用函数:
| 运算符 | 对应通用函数 | 逻辑含义 |
|---|---|---|
| & | bitwise_and() | 与 |
| | | bitwise_or() | 或 |
| ^ | bitwise_xor() | 异或 |
| ~ | bitwise_not() | 非 |
这种布尔数组实用之处在于,可以将其作为数组索引,从而快速选出在 True 位置的所有元素。例如,以下操作可以选择数组中的所有偶数元素:
注意:这种情况下 a % 2 和 a % 2 != 0 表示的不是一个意思。前者得到的是一个数值数组,将其作为索引时每个元素表示的意思是索引值位置的元素;后者得到的是一个布尔数组,将其作为索引时每个元素表示的意思是是否取用当前位置的元素。
可以使用 where() 函数将后一种布尔数组转为等价的索引数组:
where() 函数一般用在高维的索引查询中,每个数组相应位置元素组合的结果就是元素在高维数组的索引。
通用函数高级特性
通用函数有两种表现形式:函数对象和运算符。显式使用通用函数代替运算符的好处在于,可以使用通用函数提供的一些参数。
例如,有时需要指定一个用于存放这些运算结果的数组。所有的通用函数都可以通过设置 out 参数的值来指定计算结果的存放位置:
这个特性也可用于向数组视图内输出数据。例如可以将计算结果写入指定数组间隔的位置:
对于较大的数组,使用 out 参数可以有效节约内存。
通用函数对象还提供了一些方法,可以完成更高级的运算需求。例如,调用通用函数对象的 .reduce() 方法会对给定的元素连续执行操作,直到得到单个的结果,类似 functools 库的 reduce() 函数:
类似于 itertools 库的 accumulate() 函数,可以使用通用函数对象的 .accumulate() 方法来存储每次计算的中间结果:
任何通用函数对象都可以使用 .outer() 方法获得两个不同输入数组的所有元素对的运算结果。例如:
上一节提过:当使用数组索引修改值时,如果索引数组包含多个相同的索引元素,那么只有最后一次对索引位置的操作才有效。如果想要每次使用索引时立即执行给定的操作,可以使用通用函数的 .at() 方法:
广播规则
广播规则简介
如果二元通用函数作用于两个数组,那么将对相应元素逐个计算:
这种操作很容易理解。但是二元操作也可以用于不同大小的数组,例如可以简单地将一个标量(可以认为是零维的数组)和一个数组相加:
广播规则(broadcasting rule)允许二元操作用于不同大小的数组。例如,甚至可以将一个一维数组与二维数组做运算:
广播规则并没有特别规定这两个数组的运算次序,其实质上是扩展了数组的形状,使两个数组形状匹配再做运算:当一维数组与标量运算时,标量将复制若干份形成一个形状匹配的一维数组;当一维数组与二维数组运算时,一维数组将自身复制若干份向着另一个维度扩展,从而匹配二维数组的形状。
以下是 numpy 官网提供的一个很好的图解,来表示广播时的形状扩展:
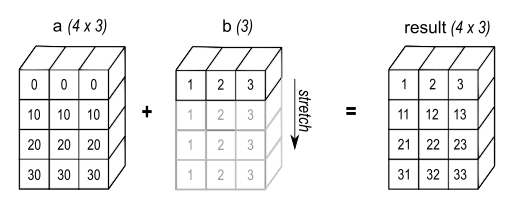
更复杂的情况涉及到对两个数组的同时广播。例如对一个行向量和一个列向量做运算:
x1 必须复制自身以扩展到二维,但 x3 也需要在第二个维度扩展以匹配出一个公共的形状。
广播规则的原理
numpy 的广播遵循一套严格的规则,这套规则是为了决定两个数组间的操作:
- 规则 1 :如果两个数组的维度不相同,那么更小维度的数组首先需要将自身提高一个维度(形状在左边补 1 );
- 规则 2 :如果两个数组的形状还是不匹配,那么数组将会沿着只有一个元素(形状值为 1 )的维度将这个元素复制若干份,以扩展并匹配另外一个数组的形状;
- 规则 3 :如果两个数组的形状在任何一个维度上都不匹配并且没有任何一个维度只有一个元素,那么会引发异常。
接下来看几个广播的示例。对于以下两个相加的数组:
| l.shape == (2, 3) | r.shape == (3,) |
根据规则 1 ,数组 r 的维度更小,因此需要提升一个维度(在其左边补 1 ):
| l.shape == (2, 3) | r.shape => (1, 3) |
根据规则 2 ,第一个维度不匹配,因此扩展该维度以匹配数组:
| l.shape == (2, 3) | r.shape => (2, 3) |
现在两个数组形状匹配了,最终结果也就是该形状。
再来看一个示例,对于一个行向量和一个列向量:
| l.shape == (3, 1) | r.shape == (3,) |
根据规则 1 ,在数组 r 的左边补 1 :
| l.shape == (3, 1) | r.shape => (1, 3) |
根据规则 2 ,扩展其值为 1 的维度匹配数组 l :
| l.shape == (3, 1) | r.shape => (3, 3) |
这个时候两个数组的形状仍然不匹配。不过数组 l 还有元素个数为 1 的维度,因此根据规则 2 ,继续扩展其值为 1 的维度匹配数组 r :
| l.shape => (3, 3) | r.shape == (3, 3) |
现在两个数组形状匹配了,并且得到一个公共的形状。
最后看一个类似的相加:
| l.shape == (3, 2) | r.shape == (3,) |
根据规则 1 ,同样在数组 r 的左边补 1 :
| l.shape == (3, 2) | r.shape => (1, 3) |
根据规则 2 ,在数组 r 的第一个维度进行扩展,以匹配数组l的维度:
| l.shape == (3, 2) | r.shape => (3, 3) |
现在根据规则 3 ,最终的形状还是不匹配,但是也没有任何一个数组的维度值为 1 ,因此这样的两个数组相加会产生错误: