数据结构05-散列

数据结构与算法 2022年8月10日

散列的概念

散列简介

前文介绍的树或链表都是一种链式存储结构，在获取某个位置的节点时都需要沿着路径依次查找下一个节点的位置，而不能直接定位。

数组（或者说顺序存储的线性表）则支持直接定址，如果知道一个元素在数组中的位置，则可以直接通过地址偏移得到，该过程可以以常数级且非常快的时间运行。例如，假设将某班学生的信息按学号排序放在数组中，那么只需要知道学生学号，就可以立即访问数组的对应位置，从而获取学生信息。

散列表(hash table)就是根据该原理实现的。散列表也叫哈希表，可以为不同值（这个值可以是任意类型的，包括浮点数、字符串等）在散列表中分配一个地址，但这个值不能直接得到，而是要经由一定计算从而转换为整数。该映射关系由散列函数计算。

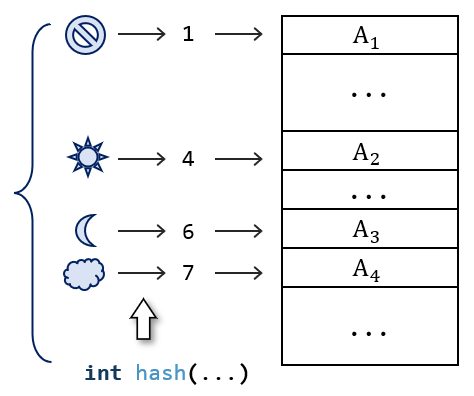
理想的情况下每个元素的映射关系易于计算，且每个元素都能被分配到唯一的地址。例如假设机器中拥有一个很长的结构数组，索引值位置存放身份证号对应的个人信息，那么可以根据一定规律计算得到身份证号，再根据身份证号就可以直接找到存放个人信息的单元。然而这是不可能的，因为单元的数目总是有限的，但是要存储的元素可能是无法穷举的。

散列函数

散列函数需要谨慎编写，一个好的散列函数应该能尽可能给不同的值分配不同的地址，同时又可以避免地址被浪费。除此之外，如果两个关键字计算出的地址一致，发生冲突(collision)，散列函数应当额外采取一些动作来确保散列表都能容纳它们。

考虑要为一些英文单词计算分配散列表中的地址。字符串无法直接转换为整数，需要采取一个算法。

一种简单的实现是使用字符串的 ASCII 累计值作为散列值，这样做实现简单且计算很快。不过英文字符的 ASCII 累计值一般低于 2000（只考虑小写英文字符）；而实用的英文词汇至少也得几万个，平均下来每个位置都有十多个词汇发生冲突。这显然不是一种有效的散列函数。

那么可以给每位字符的 ASCII 值乘上一个权重，且越靠后的字符权重越高。例如，可以使用多项式函数：

\\[ h_k = k_1 + 27 k_2 + 27^2 k_3 \,\dots \\]

这样可以就可以增加字符间联系的作用。相应的代码实现如下：

typedef unsigned int index;

index HashWord(const char* key, int table_size) {
    unsigned long val = 0;
    while (*key != '\0')
        val = (val << 5) + * key++;
    return val % table_size;
}

程序使用如下变式计算多项式的和：

\\[ h_k = (( \dots k_3) \times 27 + k_2 ) \times 27 + k_1 \\]

使用 32 代替 27 的原因是可以通过移位加速运算。使用取模可以减少表长度，同时提升表的利用率。使用该算法时，部分计算出的对应关系如下：

"hello"->28423
"world"->34135
"algorithm"->36119

当然，该算法还是存在许多问题，不过今天的重点不是散列算法，而是需要提出一种合适的数据结构，使得发生冲突时能有相应的解决方案。接下来就介绍两种常用的方法。

碰撞解决方法

分离链接法

分离链接法(separator chaining)将散列到同一个值的所有元素保留到一个表中。下图展示了使用链表模型下的分离链接法：

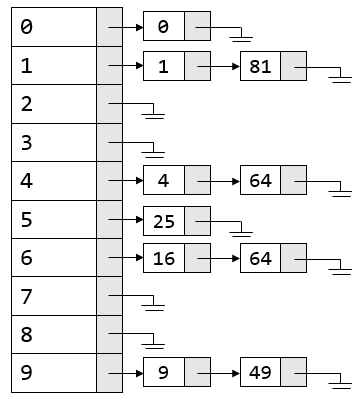
除了使用链表，还可以使用其余任意的表、二叉树，甚至是另一个散列表来保存冲突的元素。

为了执行查找，散列函数指出应该使用哪一个表。如果表的个数较多且散列结果较平均，遍历表并不需要检查多少元素，总体效率还是不错的。

为了执行插入，同样需要遍历表以确认元素是否已经在表中；如果还未存在，则可以插入表的任意位置，取决于使用场景。

分离链接散列表的类型声明如下：

typedef linkedlist hashsep_node;
typedef struct hashsep_table {
    int size;
    hashsep_node* list;
} * hashsep_table;

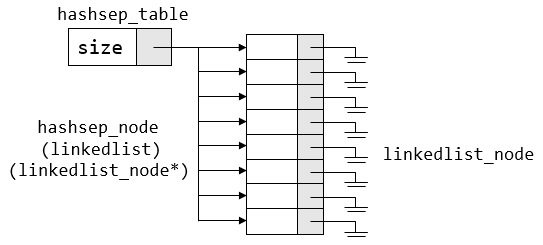
以上定义有些混乱，可以结合上面图示理解：hashsep_table 指针指向一个分离链接散列表；list 域指向表的主体部分，注意，它是一个指向指针的二重指针；hashsep_node 是一个链表，指向具体节点。下图有助于理解它们的关系：

因此，分离链接散列表的创建过程为：

hashsep_table HashSepTable_New(int size) {
    hashsep_table table = malloc(sizeof(struct hashsep_table));
    if (table == NULL)
        return NULL;      // out of memory
    table->size = size;
    table->list = malloc(sizeof(hashsep_node) * table->size);
    if (table->list == NULL)
        return NULL;      // out of memory
    for (int i = 0; i < table->size; i++) {
        table->list[i] = malloc(sizeof(linkedlist_node));
        if (table->list[i] == NULL)
            return NULL;  // out of memory
        table->list[i]->next = NULL;
    }    
    return table;
}

程序中需要为散列表、散列表链表组、散列表链表组每个链表的首个节点都分配内存。定义时链表使用了表头，因此对每个链表都需要单独调整表头。

查找操作将返回一个包含元素的链表单元。在通过散列函数取得合适的链表后，接下来的查找等同于链表的查找：

linkedlist_node* HashSepTable_Find(hashsep_table table, elemtype key) {
    linkedlist list = table->list[Hash(key, table_size)];
    linkedlist_node* node = list->next;
    while (node != NULL && !Equals(node->elem, key))
        node = node->next;
    return node;
}

注意，由于使用散列时元素的值未必可以直接比较，因此这里抽象为 Equals() 函数，字符串的具体实现可以使用 strcmp() 。

接下来是插入，如果插入的项已经存在，则什么都不用做；否则，将其插入链表的前端：

status HashSepTable_Insert(hashsep_table table, elemtype key) {
    linkedlist_node* node = HashSepTable_Find(table, key);
    if (node == NULL) {   // key not found
        linkedlist_node* new_node = malloc(sizeof(linkedlist_node));
        if (new_node == NULL)
            return 2;     // out of memory
        linkedlist list = table->list[Hash(key, table_size)];
        new_node->next = list->next;
        Assign(new_node->elem, key);
        list->next = new_node;
        return 0;
    }
    return 1;
}

插入链表前端的实现是最方便且高效的，并且有时候最新插入的元素可能最先被访问。不过该函数在查找和插入时两次调用了散列函数，如果将其合并可能会更快一些。

删除操作和链表的删除一致。很多时候散列表都没必要删除，那么不使用表头操作还会更简单一些。

如果定义散列表的装填因子(load factor) \\( \lambda \\) 为散列表中元素个数与表大小的比值。表的平均长度为 \\( \lambda \\) ，执行一次查找需要的时间为计算散列值以及遍历表所用的时间：如果不存在该元素，则遍历的链接数平均为 \\( \lambda \\)（不包括 NULL 链接）；存在该元素时，需要遍历 \\( 1 + \lambda / 2 \\) 个链接。

装填因子直接影响查找的效率。在以上链表实现的分离链接散列表中，要求 \\( \lambda \sim 1 \\) ，如果比 1 大，说明元素较多，不可避免地会加长链表；如果比 1 小的多，那么表的大小不能充分利用。

除此之外，使用素数作为表的长度也能使元素更分散一些，比如不会使相同比例的数值分到同一个模。stackoverflow 有一个问题就是关于它的，有兴趣可以看一看里面的回答。

开放定址法

分离链接法的缺点是需要指针，且新单元分配内存需要时间。开放定址散列法(open addressing hashing)是另外一种用链表解决冲突的方法。该方法在遇到冲突时，尝试选择另外的单元，直到找到可用的空单元。因此所有元素都需要直接放入表中，开放定址散列法所需要的表更大，且装填因子也不能过大。

开放定址法的查找也是如此，当发现对应位置不是该元素时，它沿着相同的选择路径继续，直到发现空的位置，就说明该元素根本没有被插入过。

更一般地，当散列函数计算出结果 \\( h_0(X) \\) 但发现该位置被占用时，它就重新计算出 \\( h_1(X), h_2(X) \\) 等，其中：

\\[ h_i(X) = (\text{hash}(X) + F(i))\mod size \\]

函数 \\( F \\) 用于解决冲突。下面介绍几个典型的函数选择。

  • 线性探测法

线性探测法中，函数 \\( F \\) 是线性函数。下图展示了这一原理：

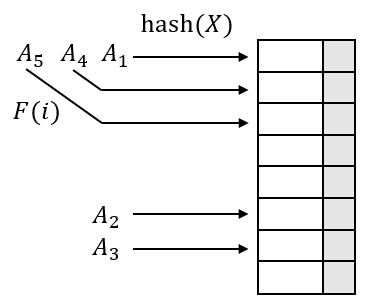
这样做的缺点是碰撞时单元会形成一些区块，导致一次聚集(primary clustering)。下一次散列到该聚集区块的值往往又需要多次线性探测，且会加重聚集区块。

计算结果表明线性探测的预期探测次数对插入和不成功的查找而言大约为 \\( 0.5(1 + 1 / (1- \lambda)^2) \\) ，对成功的查找为 \\( 0.5(1 + 1 / (1 - \lambda)) \\) 。因此线性探测法要求 \\( \lambda < 0.5 \\) ，否则当表快满时线性探测要往下找很多个节点才能找到一个空余的，浪费较多时间。

  • 平方探测法

平方探测可以解决线性探测的聚集问题。平方探测就是将冲突函数改为二次函数，下图说明了为何此过程不会聚集：

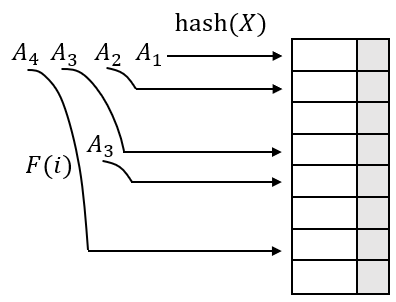
可以证明，如果使用平方探测，且表的大小是素数，那么当表至少有一半是空的时候，总是能插入一个元素。

该结论的证明需要通过一定数学公式推导。这里可以简单这么理解：当表长是素数时，在任何位置插入元素后，在不断绕回寻找可用节点时至少会有半个表被遍历到，因此只要表有一半是空的，总能找到一个合适的位置。

不过平方探测的缺点是当表被填满超过一半时，有时甚至会出现一个合适的位置都找不到的情况。这就要求其装填因子应该低于 0.5 。

以平方探测法为例，开放定址法的散列表结构声明为：

enum hashquad_status {
    HASHQUAD_USED, HASHQUAD_EMPTY, HASHQUAD_DELETED };
typedef struct hashquad_node {
    elemtype elem;
    enum hashquad_status status;
} hashquad_node;
typedef struct hashquad_table {
    int size;
    hashquad_node* list;
} * hashquad_table;

在开放定址散列表中，不能直接删除元素，否则会使定址关系断裂；如果要删除，需要使用懒惰删除策略，在定义中也增加了对懒惰删除的支持。

初始化开放定址散列表和初始化分离链接散列表的过程类似。由于不使用链表，因此这部分内容会简化一些：

hashquad_table HashQuadTable_New(int size) {
    hashquad_table table = malloc(sizeof(struct hashquad_table));
    if (table == NULL)
        return NULL;  // out of memory
    table->size = size;
    table->list = malloc(sizeof(hashquad_node) * table->size);
    if (table->list == NULL)
        return NULL;  // out of memory
    for (int i = 0; i < table->size; i++)
        table->list[i].status = HASHQUAD_EMPTY;
    return table;
}

为了执行查找操作，在查找到对应对应的表单元时，会沿着平方路径继续查找，直到找到对应的单元或发现已经到路径的结尾。结尾的标志为遇到一个 EMPTY 的项：

index HashQuadTable_Find(hashquad_table table, elemtype key) {
    index pos = Hash(key, table->size);
    int collision = 0;
    while (table->list[pos].status != HASHQUAD_EMPTY &&
           !Equals(table->list[pos].elem, key)) {
            pos += 2 * ++collision - 1;
            if (pos >= table->size)
                pos -= table->size;
    }
    return pos;
}

两个判断条件不能写反，否则当发现元素匹配时，判断短路会忽视了该位置应该不可用的事实。程序中使用平方间的关系 \\( (i+1)^2 = (i)^2 + 2i - 1 \\) 来加速运算，并在必要的时候执行绕回。

查找发现不存在时，函数会返回路径上的最后一个位置，插入例程可在返回值的基础上做插入：

status HashQuadTable_Insert(hashquad_table table, elemtype key) {
    index pos = HashQuadTable_Find(table, key);
    if (table->list[pos].status != HASHQUAD_USED) {
        table->list[pos].status = HASHQUAD_USED;
        Assign(&table->list[pos].elem, key);
        return 0;
    }
    return 1;
}

如果元素已经存在，那么就什么都不做。

  • 双散列

平方探测排除了一次聚集，但缺点是散列到同一位置上的元素将继续寻找同样的备选单元，形成二次聚集(secondary clustering)，还是会拖慢查找速度。

另一种解决冲突的方法是使用双散列(double hashing)，使用第二个散列函数往下寻找新的备选单元。这样做的优点是散列到同一位置的元素会再次散列到不同位置。

使用双散列需要谨慎选取第二个散列函数，并且会额外花费一些计算时间。

再散列

开放定址散列法要求装填因子不应超过 0.5 ，否则某些操作运行的时间将很长，甚至可能出现失败。如果当装填因子快达到该值，为了能将其降低，需要扩充表长。但不能直接对原表做扩容，否则绕回操作将会变化而导致单元间的联系断裂。

因此，需要新建一个更大的表，使用相关的新散列函数扫描原始散列表，计算每个存在的元素的新散列值并将其插入新表中。这一过程称为再散列(rehashing)，它需要耗费 \\( O(N) \\) 的时间，因此该操作只应该在必要的时候进行，例如当装填因子到达某一个特定值。

再散列的实现比较简单，只需要创建一个更大（例如两倍大）的表，然后将原表内的所有元素重新插入新表内即可：

hashquad_table HashQuadTable_Rehash(hashquad_table table) {
    int old_size = table->size;
    hashquad_node* old_list = table->list;
    table = HashQuadTable_New(NextPrime(old_size * 2));
    for (int i = 0; i < old_size; i++)
        if (old_list[i].status != HASHQUAD_USED)
            HashQuadTable_Insert(table, old_list[i].elem);
    free(old_list);
    return table;
}

近期文章

归档

京ICP备2021034974号
contact me by hello@frozencandles.fun