树的概念
树的结构
树(tree)是一种典型的一对多关系,下图展示了一棵具体的树:
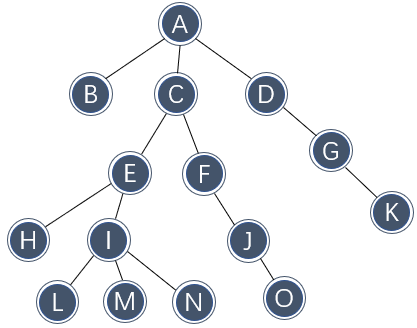
将上图倒过来看就是生活中常见的树。树从一个主干开始,随着一对多指数级分裂,向上逐渐变茂盛。
可以用多种方式定义树。常见的定义方式是递归:一棵树是一些节点的集合:若集合非空,则一棵树由根(root)节点 \\( r \\) 以及 0 个或多个非空子树 \\( T_1,T_2,\dots,T_k \\) 组成。每棵子树的根都被来自根 \\( r \\) 的一条有向的边(edge)所连接。
下图表示这种树的思想:
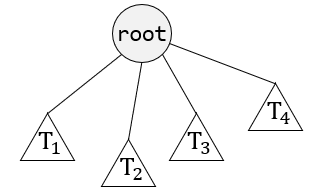
每一棵子树的根称为根 \\( r \\) 的子(child)节点,而 \\( r \\) 是每一棵子树根的父(parent)节点。
子树 \\( T_1,T_2,\dots,T_k \\) 也采用同样的方式定义,因此说这种定义是递归的。这种定义下,一棵树是 \\( N \\) 个节点和 \\( N-1 \\) 条边的集合(根节点 \\( r \\) 没有对应的边)。
以上展示的具体的树中,根为节点 A ,每一个节点可以有任意多个子节点,包括 0 个。没有子节点的节点称为叶(leaf),具有相同父节点的节点称为兄弟(sibling)。类似地可以定义祖父(grandparent)节点和子孙(grandchild)节点关系。
从节点 \\( n_1 \\) 到节点 \\( n_k \\) 的路径(path)定义为节点 \\( n_1,n_2,\dots,n_k \\) 的一个序列,使得对于 \\( 1 \leq i < k \\) ,节点 \\( n_i \\) 是 \\( n_{i+1} \\) 的父节点。这个路径的长(length)为该路径上边的条数,即 \\( n-1 \\) 。从每一个节点到它自己有一条长为 0 的路径,从根到每一个节点存在且仅存在一条路径。
任意节点 \\( n_i \\) 的深度(depth)为从根到该节点的唯一路径的长,根的深度为 0 ;高(height)是从 \\( n_i \\) 到一片树叶的最长路径的长,因此所有树叶的高度都是 0 。
一棵树的高等于它根的高;深度等于它最深树叶的深度,且等于树的高。
如果存在从 \\( n_1 \\) 到 \\( n_2 \\) 的一条路径,称 \\( n_1 \\) 为 \\( n_2 \\) 的祖先(ancestor)节点,而 \\( n_2 \\) 是 \\( n_1 \\) 的后裔(descendant)节点。如果同时 \\( n_1 \neq n_2 \\) ,那么 \\( n_1 \\) 是 \\( n_2 \\) 的一位真祖先(proper ancestor),而 \\( n_2 \\) 是 \\( n_1 \\) 的一个真后裔(proper descendant)。
以上定义看似多余且非常不直观,但它对于分析树的性能是有帮助的。后续会介绍多种不同类型的树,它们是树的实现子集,并在某些场景上可以提升效率。
树的简单实现
树的应用非常广泛,其中之一就是操作系统的文件结构。在操作系统中,一个目录可能包含几个子目录或文件,子目录中又可能包含子目录或文件,这种一对多且递归的关系就可以使用树来表示。在 Windows 系统中,在命令行中显示当前目录的体系结构使用的命令就为 tree :
以上就是一个典型的树状结构。
树的节点在逻辑上存在对应关系,那么就可以借用链表的思想,在节点中使用一些指针指向它包含的每一个子节点。只需要增加节点中指针的个数就可以从一对一连接变成一对多连接,符合树的定义。
然而实际情况下,子节点的数量不定且可能变化,因此不能直接建立对应到每个子节点的指针。既然使用链表的思想,那么可以再重新安排一下树的结构,变成如下模型:
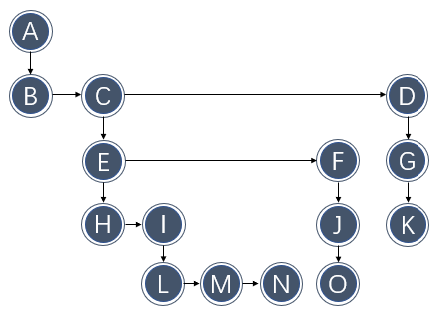
该模型下,每个结点都需要两个固定的指针:一个指针指向子树,一个指针指向兄弟节点。这样就可以以确定的方式串联起整棵树的节点了,且可以很方便地管理所有的子节点。
不过这种树的实现不具备研究价值。下面介绍一种树的子集:二叉查找树,它是一种特定的树的实现,主要优化了查找的方式,效率比表快得多。
二叉查找树
二叉树的概念
二叉树(binary tree)是一棵树,符合树的通用定义,但它要求其中每个节点都不能有多于两个的子节点。
下图展示了一个二叉树的模型,其中 \\( T_L \\) 和 \\( T_R \\) 均可能为空:
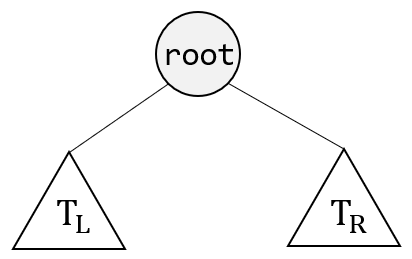
二叉树的重要性质是二叉树的平均深度为 \\( O(\sqrt{N}) \\) (二叉树节点不总是左右都有节点,因此二叉树的节点一般会随着深度线性增长),不过最坏情况(都只有一边有子节点)下深度可以达到 \\( N-1 \\) 。
由于该性质,二叉树在查找中很有用。
二叉查找树
二叉查找树(binary search tree)又是一种特殊的二叉树,它满足二叉树的所有要求,但同时规定:对于树中的每个节点 \\( X \\) ,它的左子树中的所有值小于 \\( X \\) 中的值,而它的右子树中的所有值大于 \\( X \\) 的值。
这意味着该树可以用某种统一的方式排序。在第一节就介绍了二分查找法,并指出二分查找法有远低于线性查找的时间开销。然而二分查找必须要求结构是有序的,而对线性表的排序会涉及表项的移动,移动表项总是要消耗线性的时间,因此线性表不适合直接使用二分查找。
然而二叉查找树天然是有序的,它具有链表一样的常数级插入删除开销。理想的二叉查找树左右子节点都能尽可能利用,使得节点可以随着深度指数级增长,从而使平均深度达到 \\( O(\log N) \\) 。
有了以上对二叉树模型的描述,二叉树的节点定义为:
由于二叉树最多只有两个子节点,因此不需要使用链表的方式管理子节点,可以在指针域中直接定位子节点。
树是一种一对多的关系,因此树的很多操作都需要沿着多个方向分裂执行。这种特点使树的操作比较复杂,并可能无法及时停止。
前面介绍的树是使用递归的方式定义的,那么也可以使用递归的方式操作树。这样做虽然不够直观,但可以完美贴合树的定义。
例如清空一棵树的操作,为了清空一棵树需要清空它的所有节点,但为了使树不发生断裂,需要逐层清空叶节点。如果采用循环的方式不能很好地执行回退操作,此时可以考虑使用递归。递归的实现非常简单:
在删除一棵树时,需要先删除它的左右子节点:如果存在左右子节点,就说明有子树,那么就进入左右子树递归删除;否则就说明该节点已经是树叶了,被删除也没有影响。在确保子树都被删除了以后,再删除节点自身。考虑到这里使用了双递归,还不是尾递归,因此无法很轻松地改写为循环。
递归实现下,终止条件非常重要。在清空例程中,递归的终止条件为不存在子节点,那么就停止递归,返回上一步。由于二叉搜索树的平均深度为 \\( O(\log N) \\) ,递归消耗的空间资源增长率也与其类似,不易发送空间不够的情况。
根据这种思想,可以实现查找。查找操作一般需要返回指向树中含有对应值的节点的指针(而不是一个索引)。如果这样的节点不存在,则返回空指针。
根据二叉查找树的定义,如果查找的值比当前节点的值小,那么可能的值存在于它的左子树中,就去它左子树中查找;如果值比当前节点的值大,那么就去它右子树中查找,这也很适合用递归的方式实现:
注意测试的顺序,关键问题是需要首先测试当前位置是否为空树,否则后续的查找会出现问题。同时还需要将最不可能的情况,也就是正好找到的情况放在最后一步执行。
这里同样遵循树的递归定义,并且使用的是单个的尾递归,因此可以方便地使用 while 循环实现。
可以使用类似的方法查找树的最值。由于如果存在左子树,左子树上的值总是比当前节点的值小的,因此如果要找到最小值,可以不断递归遍历左子树,直到达到最大深度为止。最大值可也用类似的方式找出。
下面给出了分别用递归和循环实现的查找最值:
查找最值的要点与普通查找类似,都要注意终止条件是树已经到达最深的位置了。除此之外,最好判断一下一开始传入的树是否为空树。
插入与删除操作
二叉查找树的插入和删除比较复杂。二叉查找树为了维持有序结构,插入和删除都不像链表那么简单,而是要将待插入的内容插入到正确的位置,这个位置一般是确定的。
插入稍微简单一些。不过需要注意的是,之前在介绍二叉查找树时都假定树中的元素都有着不同的值,如果待插入的值与某个节点的值相同,那么就要根据实际情况安排它:要么将其丢弃,要么用别的方式记录它。
插入的实现如下,一个插入例程可以在查找的基础上编写:如果找到与待插入元素相同的节点,那么就什么也不用做;否则沿着应有的路径继续向下查找,并将其插入到查找路径的最后一点上。
下图展示了这种插入思路:
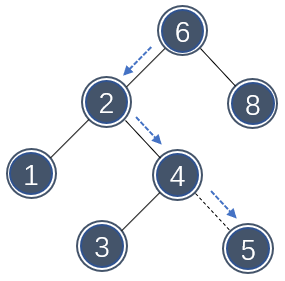
为了插入元素 5 ,尝试沿着路径搜索 5 :6(向左找)→2(向右找)→4(向右找)→找到底了,那么这个位置满足二叉查找树的要求,就将其插入这个位置上。
可见插入都是在叶节点上完成,既然使用查找的方式寻找合适的插入位置,那么下一次查找、插入时也可以顺利找到该节点,且不会使树存在重复的元素。
如果经常发生重复插入的情况,或者需要允许元素重复,可以在节点中附加一个记录频率的字段来保存该信息。这样做的优点是在删除时可以直接将频率字段减 1 ,而不需要真正移除节点,降低了实现的难度。
根据该原理,以下是插入的例程,注意还是用递归的方式实现的:
每一次递归时,都尝试到子树中执行插入;真正的插入发送在子树为空的情况(到达边缘位置了),那么就在原地创建一个新的节点并容纳插入值。为了让新的节点成为树的一部分,将该函数写成返回一个指向新根节点的指针,并在递归回退时重新建立路径上的所有指针。
删除显然是最困难的过程,为了确保删除时维持树的稳定,要考虑多种不同的情况:
- 待删除的节点是一片树叶:这种情况下删除并不会影响树的其余部分,可以立即删除
- 待删除的节点只有一个子节点:这种删除类似链表删除,只需要调整父节点的指针绕过该节点,指向子节点即可
下图展示了删除的节点只有一个子节点的情况:
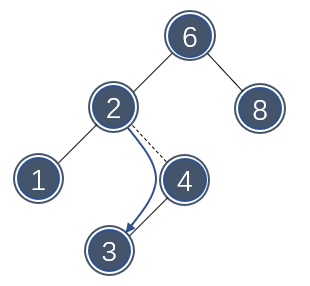
删除前后,整个树的结构仍然符合二叉查找树的定义。
- 待删除的节点有两个子节点:这是真正复杂的一种情况,因为不但要删除对应节点,还需要安排它的两个子节点到合适的位置
这种情况下,一般的删除方法是用其右子树中最小的数据代替该结点的数据,然后再递归去除右子树中该最小数据。由于右子树中最小的数据也比左子树中的任意节点大,因此这样的操作既能去除该节点,同时符合二叉查找树的定义。
下图展示了从一棵较为复杂的树中删除值 4 的情况:
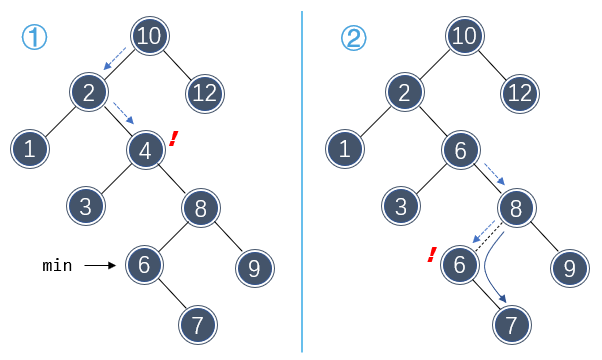
该删除分几步:首先找到节点 4 ,并用右子树中最小数据 6 代替;然后还需要删除右子树中重复数据 6 ,那么继续沿着该路径查找 6 ,找到后以相同的方式删除 6 。这里右子树中的 6 只有一个子节点,因此只需要像链表一样删除即可。
删除完成之后,总体看下来,仍然符合二叉查找树的定义。
二叉查找树删除的原理其实不算太复杂,但难点在于如何实现。每一步不仅需要分析子节点个数,总体还需要满足递归的要求。
二叉查找树删除的例程如下:
以上函数可以分为几个部分:最前面用于递归查找待删除元素,如果找到了判断子节点个数:如果有两个子节点,查找右侧最小值替换该位置,并再次递归地查找、删除该最小值;如果有 0 个或 1 个子节点,那么就按正常的方式删除。
可以预见的是,删除过程会越来越向深的方向进行,并总会遇到边缘位置(不全有两个子节点),这也就是递归终止的条件。
以上程序中,每次删除时还需要先查找出最小值替换节点,然后还要查找删除该最小值。这两步有些重复了,可以将其结合以提高运行效率,不过程序可能还会复杂一些。
效率分析
直观上看,除了清空操作外,对二叉查找树的搜索、插入、删除(插入与删除都基于查找实现)都花费 \\( O(\log N) \\) 的时间。因为每次用常数时间在树中降低一层时,就会排除剩余的一半节点。
严格来说,二叉查找树的时间花费与深度相关,如果 \\( d \\) 是包含访问值的节点深度,那么操作将花费 \\( O(d) \\) 时间。然而,实际情况下看,二叉查找树的深度并没有达到理想的平均情况。其原因出在删除操作,该操作总是用右子树中的一个节点代替原有节点,这就会造成:
- 右子树少了一个节点,并且随着递归删除,删除节点的位置越来越往右下
- 原先节点的值变大,下一次插入的位置可能会变到左边
因此,该删除操作有助于使左子树变深,右子树变浅。在足够多的随机插入和删除操作下,一棵树会不可避免地左沉:
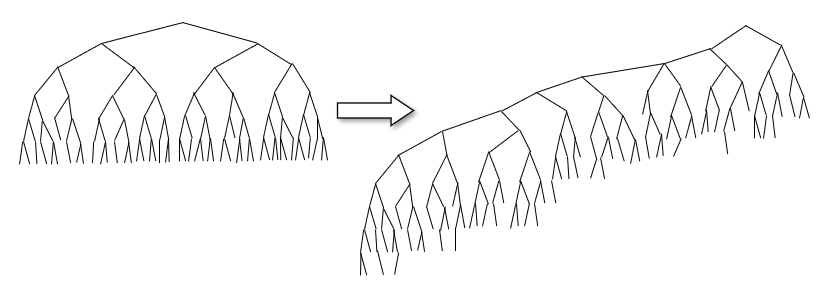
左沉使右侧节点的利用率变低,不能很好地利用两个子节点位置。一种极端的情况是每个节点的右节点都没有值,那么二叉树将会退化为有序的链表,使得深度变为 \\( N-1 \\) 。可以证明,如果随机交替插入和删除 \\( N^2 \\) 次,那么树的期望深度为 \\( \sqrt{N} \\) 。
如果能对左沉的树重新编排节点的位置,那么有助于缓解这一情况。例如,对以上删除示例中使用到的左沉的树重新排列节点后,树的深度从 6 减少为了 4 :
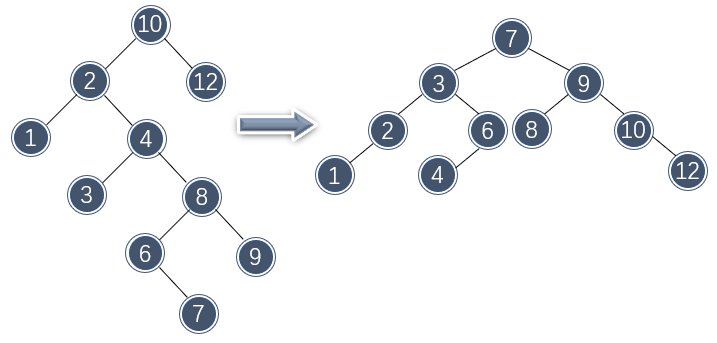
如果在删除时随机选择右子树的最小元素或左子树的最大元素来代替它,确实有助于缓解倾斜问题。不过在条件不好的情况下,还是可能发现倾斜。这就要求树必须要能够有简单的方式做调整,使得后面操作效率更高。
下面介绍一种二叉查找树的改进版本,它优化了对自调整的支持,
AVL树
AVL树的概念
AVL(Adelson-Velskii and Landis)树是带有平衡条件的二叉查找树。平衡意味着每个节点子树的高度要相近(完全等高太严格也难以实现),使整棵树不会明显倾斜,拥有接近 \\( \log N \\) 的高度。
一棵 AVL 树每个节点的左子树和右子树的高度最多差 1(空树的高度定义为 -1 ),并在每一个节点中保留高度信息。
调整树会消耗一定时间,这就要求不能太过频繁地调整,或一次只调整树的一部分。插入操作一定会破坏 AVL 树的完整性,因此可以在插入后对周围的节点做一定的调整,使其恢复 AVL 树的性质。对 AVL 树的修正可以使用旋转(rotation)来完成。
下图是一棵平衡的 AVL(子)树,因为左右子树的高度只差 1 。然而,对左侧子树的插入会破坏该平衡。插入有两种情况:一种是发生在“外侧”的插入,另一种是发生在“内侧”的插入。对右子树的插入实质上的对称的,虽然需要使用不同的代码处理。
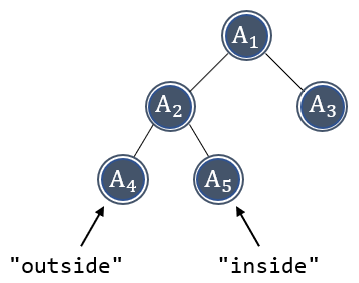
发生在“外侧”的插入可以通过对树的一次单旋转(single rotation)调整,发生在“内侧”的插入可以通过对树的一次双旋转(single rotation)调整。本节介绍旋转的基本原理,并给出简单的代码实现。
首先,采用以下代码实现 AVL 树并计算节点的高度:
接下来介绍旋转操作。
AVL树的旋转
AVL 树的旋转分为单旋转和双旋转两种,分别调整不同的不平衡情况。
- 单旋转
下图展示了一个不平衡树的抽象模型,对 \\( X \\) 节点的插入使 \\( Z \\) 明显不平衡:
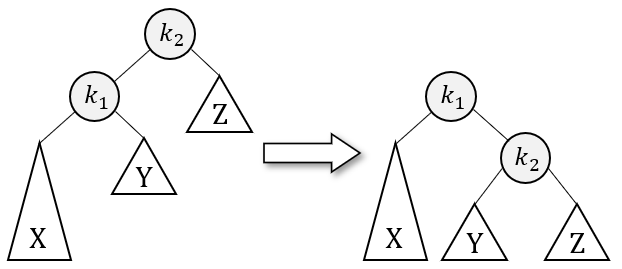
为了恢复树的平衡,需要调整两者的位置。但是为了满足二叉查找树的定义,不能直接交换它们,而是需要调整节点间的指向关系,使水平位置满足 \\( [X, k_1, k_2, Z] \\) 的顺序。
可以将单旋转看成一个不平衡的杠杆,为了使其恢复平衡,需要将支点的位置移到更靠近重心处。
以下给出了单旋转的代码实现:
对指针指向的修改可以参照旋转模型实现。在修改后还要调整节点高度,为子节点最大高度多一层。
以上介绍的是左侧插入的单旋转,另一侧的单旋转可以通过镜像操作实现。
- 双旋转
单旋转对“内侧”的插入无效,下面通过实际情况展示了这样失败的原因:
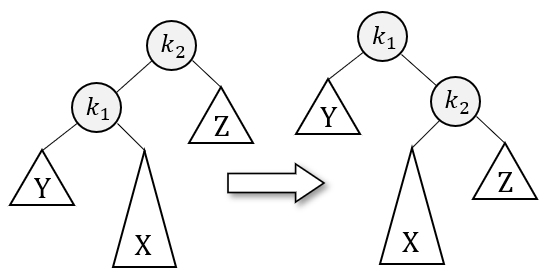
“内侧”插入模型可以看作一个天平,不平衡之处发生在中心,因此不能通过调整两端节点达到平衡。
以下模型展示了使用双旋转修复 AVL 树的方法:
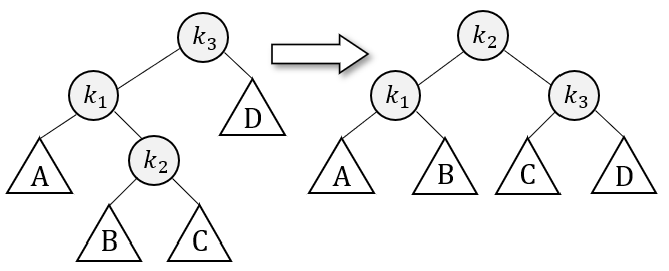
插入可能发生在 \\( B \\) 或 \\( C \\) 位置。为了重新平衡,必须让靠“中间”的节点,即 \\( k_2 \\) 作为新的根。
双旋转操作下,不管插入的位置发生在 \\( B \\) 还是 \\( C \\) ,旋转之后树总是平衡的。
双旋转操作可以以一种简洁的形式完成。下图展示的树由于插入了节点 3 ,而使 10 的两个子节点高度差 2 变得不平衡。但如果对 10 的左节点做一次右单旋转:
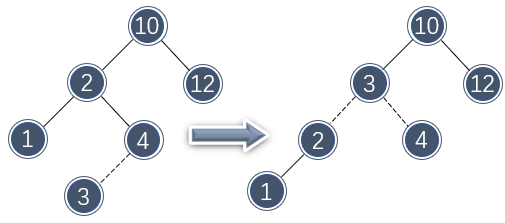
尽管还是没有平衡,但是这次的不平衡好像插入变到了“外侧”去了,那么只需要再对 10 做一次单旋转即可维持平衡:
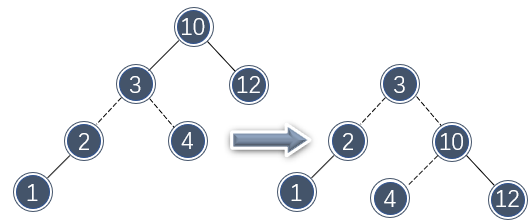
因此,代码可以以一种很简单的形式实现:
所有的旋转都只需要调整几个指针和高度,都是常数级的。
有了旋转的操作之后,就可以对 AVL 树做插入。插入毫无疑问非常复杂,因为它是在二叉查找树的插入基础上完善的。为了将 \\( X \\) 节点插入到一棵 AVL 树 \\( T \\) 中,需要递归地将其插入 \\( T \\) 的子树 \\( T_{LR} \\) 中。如果 \\( T_{LR} \\) 的高度不变,那么插入完成;否则出现高度不平衡的情况,要适当做旋转。
下面展示了插入的代码实现:
以上使用递归实现,代码是在二叉查找树的基础上扩充实现的,主要增加了高度的计算和旋转的操作,旋转发生的条件可以参考模型。
对 AVL 树删除的实现很复杂,因此这里不再介绍。如果删除不频繁的情况下,一般采取懒惰删除(lazy deletion)的方式,即在节点中附加一个额外的域,当删除时在该域中做标记或使频次减 1 。
树的遍历
由于前文介绍了树的清空操作,它就是一种遍历。因此遍历打印树可以通过类似的方式完成。
下面给出了一种至少能看的打印操作:
将相邻层顶点之间用线连接,即可看到一棵抽象的二叉查找树:

打印结果从上到下是有序的,说明二叉查找树也是有序的,因此可以换来大量数据时很快的查找效率。并且不管节点间深度有什么关系,值小的节点一定排在值大的节点的左边(图中表示为上面),因此对二叉查找树的修改一定也要维持这种规律。
打印的遍历是先处理左边节点,然后处理自身再处理右边节点,这种遍历称为中序遍历(inorder traversal),其特点是元素可以按顺序处理;而清空的遍历需要处理完两个子树后再处理自身,这种遍历称为后序遍历(postorder traversal),特点是从下向上逐层遍历。
第三种常用的遍历方式是先序遍历(preorder traversal),当前节点在子节点前优先处理,可以用来利用节点深度标志标志每一个节点:
总的来说,二叉查找树是一种比较经典的数据结构,它提出了一种较为高效的查找解决方案。二叉查找树并不是唯一的查找树,还有许多类似的、甚至更高效的查找树实现。不过对树的介绍暂时告一段落,接下来研究散列表,它实现了一种更快速的、常数级的查找,不过其限制也更大。