一元线性回归
线性回归(linear regression)应该是最简单的机器学习模型了。例如,以下是 1965~2021 年一次能源消耗量变化:
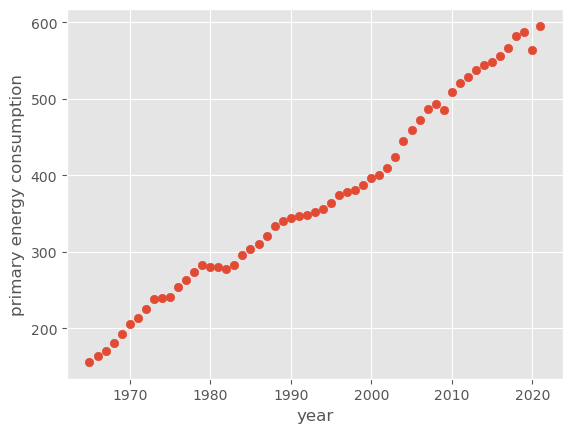
容易看出自变量(年份)与因变量(一次能源消耗量)之间大致沿一条直线分布。线性回归模型就是利用线性拟合的方式,寻找自变量与因变量背后的回归直线(趋势线),再利用回归直线做简单的分析和预测。
线性回归根据特征变量(自变量)来预测反应变量(因变量)。由于以上的特征变量只有一个(一次能源消耗量),因此这种线性回归模型称为一元线性回归。在本文最后会考虑多元线性回归的情况。
数学原理
以上的样本分布规律大致成一条直线,因此可以使用直线的公式来描述它们:
其中 \\( x \\)为自变量,\\( y \\) 为因变量,\\( a \\) 为回归系数(斜率),\\( b \\) 为截距。
为了发现自变量与因变量之间的关系,需要提供一系列因变量的实际值来拟合。对于每个自变量,其实际的因变量值 \\( y_i \\) 与预测值 \\( \hat y_i \\) 之间的接近程度可以用它们的残差平方和(Sum of Squares for Error, SSE),即差值的平方来衡量:
如果将上式展开,可以得到:
当残差平方和最小时,说明该拟合直线最能描述实际样本的线性关系。通过对上式求导并令导数为 0 ,可以得到最小的残差平方和,即拟合最优时的回归系数 \\( a \\) 和截距 \\( b \\) 。
这种求导的过程非常简单,即便手工计算也非常方便。以上计算回归直线的方法称为最小二乘法。接下来看看如何使用代码搭建线性回归模型。
代码实现:使用Scikit-Learn工具包
Python 有许多提供各种机器学习算法的第三方库,Scikit-Learn 是使用最广泛的一个。相比其它的机器学习库,它具有以下优点:
- 模型广泛,涵盖目前各种主流机器学习算法
- 使用 NumPy 实现,在计算效率很高的同时能很好地融入 Python 科学计算的生态中
- 完善的在线文档,帮助初学者快速入门
- 设计得当 API 。Scikit-Learn 的所有模型都遵循几乎相同的面向对象接口,这种高度统一的 API 让使用者无需记住每一个模型是如何实现的,只需要知道算法原理和需要设置的参数即可。许多新提出的模型也采用了相同的 API 设计,从而避免了用户熟悉库操作的成本
通过 Scikit-Learn 库可以便捷地调用一元线性回归模型。该库可以直接通过 pip 命令安装:
然后可以在命令行中导入并检查安装的版本:
在 Scikit-Learn 中,用于建立模型的基本数据集以二维数组表示,其中每一行表示数据集中的每个样本,而列表示构成每个样本的相关特征。因此这样的数组具有形状 (n_samples, n_features) ,也称为特征矩阵(features matrix)。这和 Pandas 的 DataFrame 是一致的,因此可以直接使用 DataFrame 来表示数据集。
特征矩阵常用变量 X 来表示。以上数据中自变量是一个一维数据,如果要将这些数据使用 Scikit-Learn 的线性回归模型处理,需要将每一个元素变成一个单元素数组:
包括线性回归在内的许多模型都需要通过研究自变量和因变量的关系,来预测新加入样本的值。因此除了特征矩阵 X 之外,还需要为每个样本准备一个对应的结果(目标数组),通常简记为 y。目标数组一般是一维数组,其长度就是样本总数 n_samples ,因此可以使用一维的 NumPy 数组或 Pandas 的 Series 表示。
有了数据以后,就可以用其建立模型了。在 Scikit-Learn 中,每个模型都是一个 Python 类。在建立模型前,需要从对应的模块中导入需要的类:
建立一个具体的模型就是实例化类。有一些重要的模型参数必须在应用于数据集前便确定好,这些参数通常被称为超参数,通常在初始化方法中作为参数传入。
一个模型的超参数可能有几十个,好在 Scikit-Learn 为大多不常用的超参数都提供了合适的默认值。只要调整少量的主要超参数即可。例如,假设线性回归模型需要一并拟合直线的截距,可以在初始化时设置超参数 fit_intercept 为 True :
在初始化模型以后,需要将数据集应用到其中。这一步可以通过模型的 .fit() 方法实现:
LinearRegression()
该方法会根据提供的特征矩阵和目标数组完成必要的计算,计算完成后可以得到一些模型参数。这些模型参数一般都以单下划线结尾的实例属性表示,例如线性回归模型常用的结果有回归直线的斜率和截距:
利用搭建好的模型,可以使用 .predict() 方法根据一个新的自变量预测因变量的值:
这一步等价于将新的 \\( x_i \\) 代入方程 \\( y=ax+b \\) 中求解。注意自变量同样需要写成二维数组的模式。从预测结果中可以看到 10 年、50 年和 100 年后的一次能源消耗量。
如果在一个区间内尝试预测足够多的点,并将预测结果绘制出来,就可以看到一条趋势线了:

可以看到模型中 .predict() 依据的原理就是从趋势线上选择对应的点。
结果分析
以上建立了线性回归的模型并对新的数据作出预测。但是还需要对模型的结果做一些分析。
首要的问题是数据能否应用与线性回归模型。以上的数据较为清晰地呈现出一条直线,但很多时候却未必。例如,以下是一个对看似为线性的数据应用线性回归模型的结果:
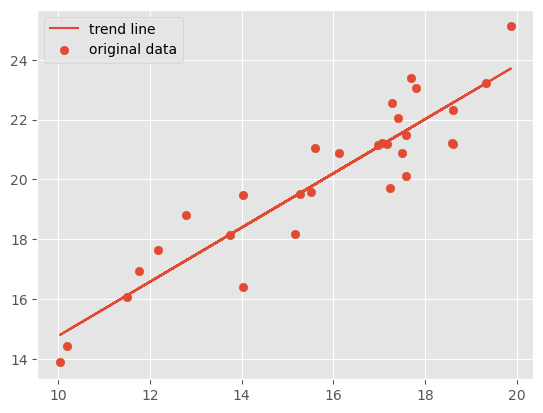
线性回归的模型评估主要以3个值进行作为评价标准:R-square(即 \\( R^2 \\) )、Adj. R-square(即 \\( \text{Adjusted}\, R^2 \\)) 和 \\( P \\) 值。对于一元线性回归,主要关心的是它的 \\( R^2 \\) 值。
设 \\( Y_\text{i} \\) 为实际值,\\( Y_{\text{fitted}} \\) 为预测值,\\( Y_{\text{mean}} \\) 为所有散点的平均值,则数据的整体平方和 \\( \text{TSS} \\) 、残差平方和 \\( \text{RSS} \\) 以及解释平方和 \\( \text{ESS} \\) 可以根据以下公式计算:
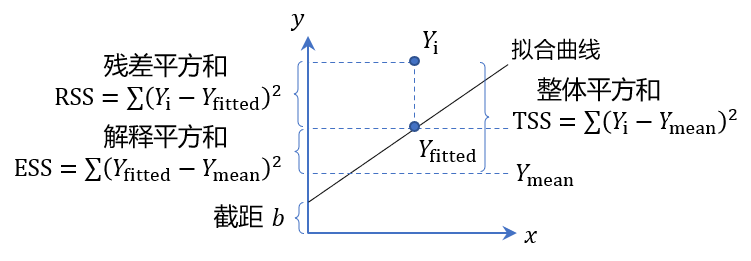
对 \\( R^2 \\) ,有如下计算公式:
对于线性回归模型,如果拟合度较高,则残差平方和 \\( \text{RSS} \\) 需要尽可能小,即 \\( R^2 \\) 尽可能大。为了避免数据的数量级对结果的影响,需要将其与整体平方和 \\( \text{TSS} \\) 对比,当 \\( R^2 \\) 趋向 1 时,说明 \\( \text{RSS} \\) 远小于 \\( \text{TSS} \\) ,即基本所有点落在回归直线上。
Scikit-Learn 自带的函数就可以计算 R-square 值,如下:
metrics 是 Scikit-Learn 包含的一个模块,里面有各种计算用的函数。为了后续分析其它指标的方便,接下来再介绍一个用于分析模型的工具。
statsmodels 是一个探究数据统计模型的 Python 第三方库。可以通过 pip 直接安装它:
然后可以通过以下代码分析搭建回归模型的各种数据信息:
| Dep. Variable: | consumption | R-squared: | 0.986 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.986 |
| Method: | Least Squares | F-statistic: | 3962. |
| Date: | Sat, 26 Nov 2022 | Prob (F-statistic): | 6.12e-53 |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | -1.473e+04 | 239.859 | -61.398 | 0.000 | -1.52e+04 | -1.42e+04 |
| year | 7.5747 | 0.120 | 62.941 | 0.000 | 7.333 | 7.816 |
| Skew: | -0.436 | Prob(JB): | 0.151 |
|---|---|---|---|
| Kurtosis: | 2.087 | Cond. No. | 2.41e+05 |
OLS 表示普通最小二乘法(Ordinary Least Squares),用于分析线性回归模型的各种统计值。sm.add_constant() 函数是为了给原来的特征变量 X 添加常数项,即公式 \\( y=ax+b \\) 中的截距 \\( b \\) 。
以上结果省略了部分不重要的数据,主要的结果已经用红色强调出了。在左上角就是模型的 R-square 值。在不同应用场合下 R-square 值的标准也不一样,一般在 0.7 以上就可以认为具有较好的线性相关性,0.9 线性相关性已经很强了。本数据的 R-square 达到了 0.98 ,完全可以认为一次能源消耗量和年份有着很强的线性关系。
线性回归模型的拓展
多元线性回归
除了一个自变量的直线拟合,还可以处理多个自变量的线性回归模型。多元线性回归是推广到多个特征变量的线性回归模型,可以考虑多个因素对目标结果的影响。
多元线性回归可以表示为如下所示的公式:
其中 \\( x_i \\) 为不同的特征变量,\\( \theta_i \\) 为这些特征变量前的系数(影响因素),\\( \theta_0 \\) 为常数项。这个数学公式表示的是三维空间中的一个平面,或者是更高维度的一个超平面。
多元线性回归也可以表示为如下的矩阵形式:
这里 \\( \boldsymbol{\theta} \\) 是模型的参数矩阵,\\( \boldsymbol{X} \\) 是特征变量向量。因此多元线性回归的模型和一元线性回归是类似的,只是训练时用的 X 每个数组内的元素不止一个而已。
多元线性回归模型的的原理也是取合适系数,使残差平方和
最小。
数学上主要通过最小二乘法和梯度下降法来计算合适的系数。
接下来通过一个具体的示例介绍多元线性回归的分析。假设某公司不同时期的利润(因变量)与各成本(自变量)之间的关系为:
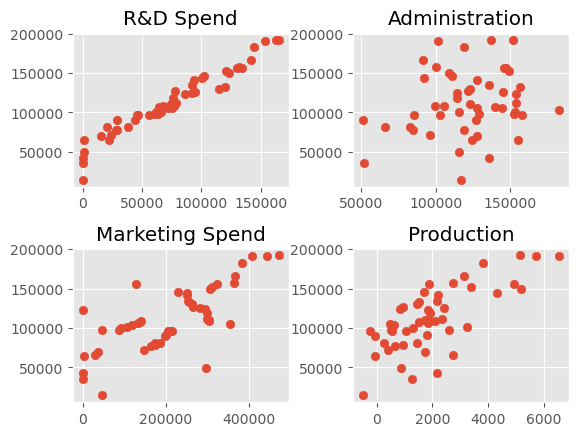
在建立模型前,首先需要分析数据是否可以建立多元线性回归模型。对于多元线性回归,衡量结果好坏的评估值还有两个:Adj. R-square 和 \\( P \\) 值。
Adj. R-square 是改进的 R-square ,目的是防止选取特征变量过多导致 R-square 值虚高。Adj. R-square 在 R-square 的基础上考虑了特征变量的数量这一因素,其公式为:
其中 \\( n \\) 为样本数量,\\( k \\) 为特征变量数量。因此选择的特征变量越多,对 Adj. R-square 影响便越大。
\\( P \\) 值是统计学假设检验的一个概念,表示假定特征变量与目标变量有显著相关性时,所得到的样本出现不符合假设的结果概率:若概率越大,则 \\( P \\) 值越大,说明特征变量与目标变量有显著相关性的可能性便越小;若 \\( P \\) 值越小,说明更可能有显著相关性。统计学中通常以 \\( P \\) 值 0.05 为特征变量与目标变量是否有显著相关性的阈值。
总体来说,线性拟合常用的几个评价标准为:
- R-square 和 Adj. R-square 衡量线性拟合的优劣
- \\( P \\) 值衡量特征变量的显著性
接下来使用 statsmodels 来检验多元线性回归的数据:
| Dep. Variable: | Profit | R-squared: | 0.952 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.948 |
| Method: | Least Squares | F-statistic: | 222.3 |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 5.009e+04 | 6571.034 | 7.622 | 0.000 | 3.69e+04 | 6.33e+04 |
| R&D Spend | 0.7762 | 0.054 | 14.442 | 0.000 | 0.668 | 0.885 |
| Administration | -0.0280 | 0.051 | -0.548 | 0.586 | -0.131 | 0.075 |
| Marketing Spend | 0.0270 | 0.016 | 1.639 | 0.108 | -0.006 | 0.060 |
| Production | 1.2157 | 1.204 | 1.010 | 0.318 | -1.209 | 3.641 |
在以上结果中,R-square 和 Adj. R-square 都达到了 0.9 以上,说明模型的线性拟合程度很好。在几个特征变量内,只有 R&D Spend 的 \\( P \\) 值达到了阈值 0.05 以内,说明利润与研发费用具有很强的线性相关性;产量和管理费用的 \\( P \\) 值都很大,说明它们与利润不太可能有线性相关性,在建立回归模型时可以忽略它们。
多项式回归
很多时候数据在散点图中未必表现为一条直线,那么就不能使用直线的方程去描述它,否则会产生欠拟合:模型没有捕捉到数据的特征,不能用于拟合数据,如图所示:
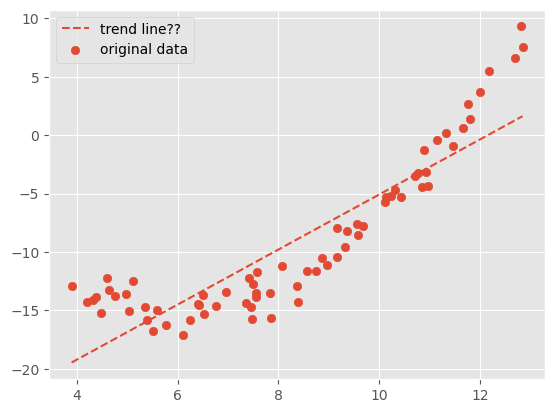
对于曲线数据,可以通过基函数对原始数据添加新的特征,使其由 \\( [ \, x \, ] \\) 变换为形如 \\( [ \, 1, \, x, \, x^2, \dots, x^n \, ] \\) 的多项式组合形式,从而将变量间的线性回归模型转换为非线性回归模型。其中第一列 1 为常数项,它的值对分析结果没有影响。
preprocessing 是 Scikit-Learn 的一个模块,提供数据预处理所需要的工具,其中就包含多项式变换的功能:
可以将变换得到的数据应用到线性回归模型中:
LinearRegression()
这样得到的回归趋势线就是一条拟合程度较好的曲线了:
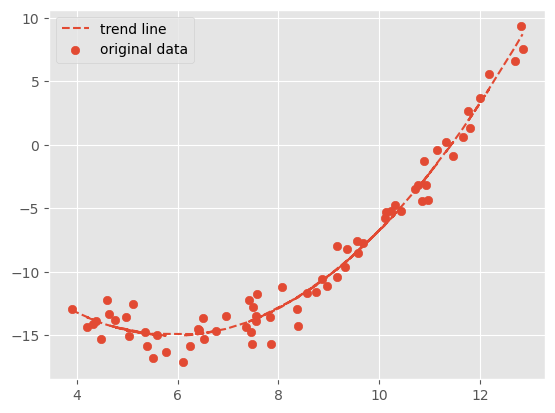
除此之外,还可以将预处理和建立模型结合起来,使用 Scikit-Learn 提供的管道操作组合成一个模型,这样便无需频繁处理数据了:
正则化线性模型
多项式回归等曲线回归模型都存在一个问题,那就是曲线的形状不易确定。例如,多项式回归的次数往往不易确定,如果设置了过高的多项式次数,可能会导致很糟糕的拟合结果。
例如,以下是对一组曲线数据分别应用 3 次和 16 次多项式的拟合结果:

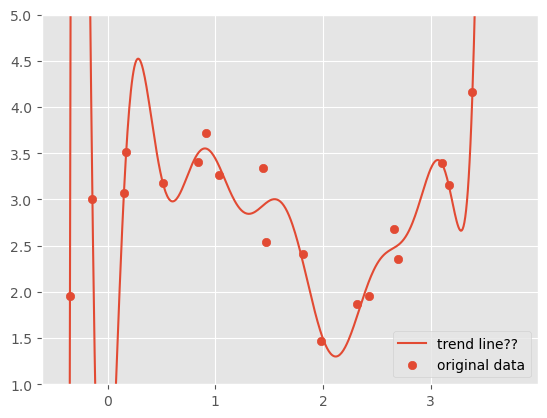
尽管 16 次多项式拟合后曲线更贴近原始数据,但并不能说明这就是一个合适的趋势线:不能为了盲目增加 \\( R^2 \\) 而增加回归曲线的次数,否则可能发生过拟合,这是一个与欠拟合相对应的概念,得出的数据不具有推广性。特别是在横坐标接近 0 的位置曲线有很大幅度的变动,这显然是不合理的。
由于残差平方无法判断是否会发生过拟合,减少过拟合的一个方法是对该公式添加额外的约束项,即正则化(regularization):更多的约束可以防止模型的某些参数不正确地过分增大而发生过拟合。
正则化的常用方法有两个:岭回归和 Lasso 回归。
岭回归(ridge regression)也称为 Tikhonov 正则化,它在描述模型最优方案的公式(残差平方和)额外添加了一个约束项:
参数 \\( \alpha \\) 用于控制约束效果:趋向于 0 的参数约束的力度更小。从公式上看,使用岭回归可以避免线性模型为了盲目贴近数据而采用很大的多项式系数 \\( \theta_i \\) 而导致曲线过于陡峭。
岭回归也和线性回归放在同样的模块内,并遵循类似的接口规则:
Ridge(alpha=0.2)
下图展示了不同参数下岭回归的结果:
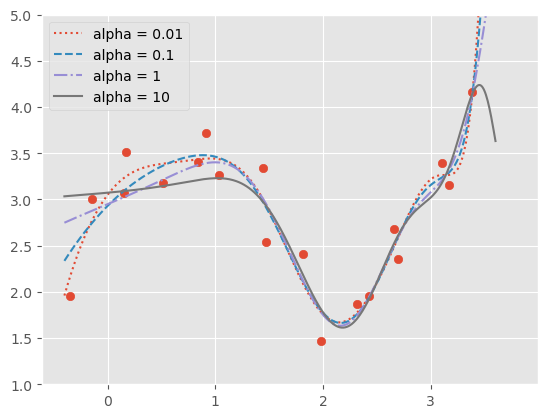
另一种常用的正则化是 Lasso 正则化,它的约束项为:
从公式上看,Lasso 回归与岭回归差别不大,但 Lasso 回归在数学上更倾向于将特征系数设置为 0 。假设有两个特征变量,那么 Lasso 回归在降低正则化项的和时,更容易接近坐标轴而使某个系数趋近 0 ,如下图所示:

可以从同样的地方导入 Lasso 类建立模型。下图展示了不同参数下 Lasso 回归的结果,可以看到都比较趋近于 3 次多项式:

总的来说,线性回归作为统计学中常用的一个工具,它的数学原理已经被研究得很透彻了,因此模型的可解释性很强,且计算速度快,对于线性数据的预测结果很好。但是线性回归不适用于非线性数据,且无法处理分类问题,因此需要提前判断数据是否有线性关系。



近期评论