聚类就是将样本划分为由具有类似的特征组成的多个类。在实际分析一堆数据时,往往会只给出这些数据的特征变量,但不知道这些数据应该如何分类,这就需要对已有数据根据性质分组。
聚类有两种常用的算法:KMeans 和 DBSCAN 。
KMeans算法
算法原理
KMeans 算法是最简单、最容易理解的聚类算法,其中 K 代表数据,Means 代表每个类别内样本的均值。顾名思义,它是用数据的均值对其分类。
例如,对于如下散点的分布,可以比较清晰地看出来它大致聚为四个集群:
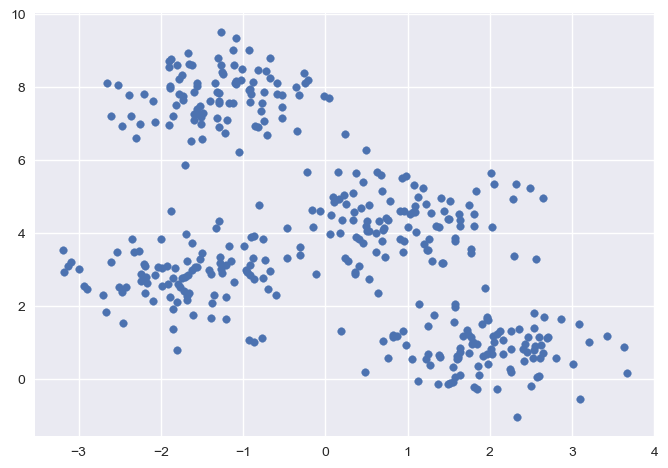
之所以可以看出它们形成了四个集群,因为每个集群都围绕着一个中心点分布,如果点离这个中心的距离更近,那么就容易看出该点属于这个集群。
这就是 KMeans 算法的原理,KMeans 算法以距离作为样本间相似度的度量标准,将距离相近的样本分配至同一个类别。通常可以采用两点间的直线距离(欧几里得距离)来度量各样本间的距离。
KMeans 算法最重要的就是计算中心点。直接计算中心点的话计算量很大,而且处理较为复杂。因此,KMeans 使用一种称为期望最大化(expectation-maximization, E-M)的算法来处理这个问题。期望最大化算法应用于数据科学的很多场景中,KMeans 是该算法的一个非常简单并且易于理解的应用。
期望最大化算法包含以下步骤:
- 期望步骤(E-step):将样本点分配给最近的集群中心点代表的类别,更新每个点是属于哪一个集群的期望值
- 最大化步骤(M-step):将集群中心点设置为该集群所有点坐标的平均值,得到集群关于中心点拟合函数最大化时对应的坐标
最开始的中心点可以通过在现有点中随机选取得到。每一次重复期望最大化步骤都将会得到更好的聚类效果,直到前后两次分类结果没有差别为止。
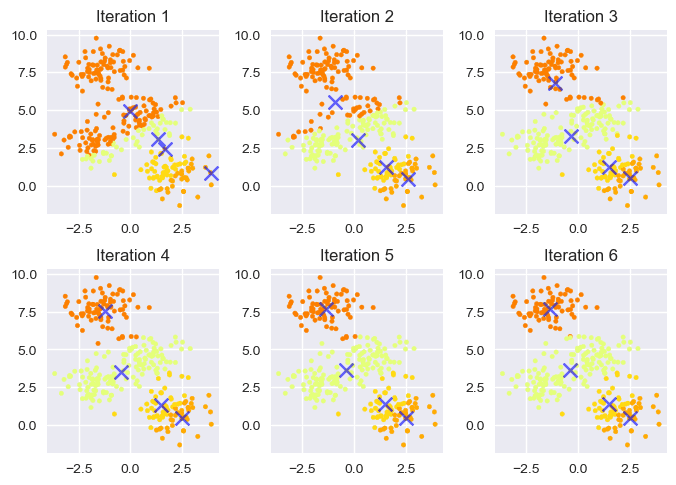
下图展示了 KMeans 聚类时的可视化迭代过程:

也可以借助可视化网站 https://www.naftaliharris.com/blog/visualizing-k-means-clustering/ 交互式查看 KMeans 算法聚类的过程。该网站还给出了许多其它算法的交互式演示,包括接下来介绍的 DBSCAN 聚类算法。
代码实现
以上介绍了 KMeans 的原理。在实际应用中,可以直接使用 Scikit-Learn 提供的工具完成 KMeans 聚类,它与 Scikit-Learn 其它工具的接口是一致的。KMeans 模型的主要参数 n_clusters 即 K 值,表示样本聚成的类数:
当聚类完成后,可以使用 .labels_ 属性获取聚类结果,.cluster_centers_ 属性获取每一个类别的中心点。
以下将所有样本点和聚类的中心点以散点图的形式表现出来,并根据聚合成的不同类别以不同颜色区分结果:
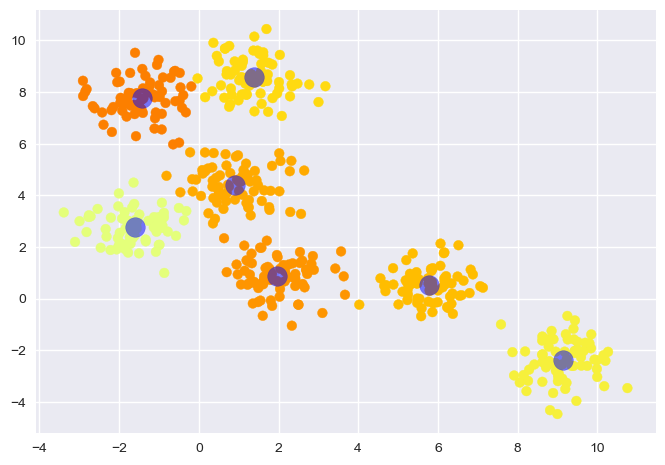
结果整体来说划分良好。
结果分析
由于 KMeans 算法是一种期望最大化算法,它会在每一步中改进结果以向着更优解的方向移动,但是这并不保证可以到达全局最优解。初始中心点的选择会在较大程度上影响聚类结果,某些随机值带来的初始中心点可能会导致仅收敛到局部最优解,但整体聚类结果并不理想:
基于此,Scikit-Learn 的 KMeans 模型提供了 n_init 参数,用于多次使用不同的随机种子运行模型,并选取最好的结果。该参数的默认值是 10 ,即从 10 次不同的测试中选择最好结果。
多次运行还需要分析哪个是最好结果,评价 KMeans 模型的一项常用的指标是各个点到聚类中心距离的平方和,称为惯性(inertia)或 WSS(Within-Cluster-Sum of Squared)。在聚合成相同数量的集群时,WSS 越小,则说明模型越好。在建立模型后,可以使用 .inertia_ 属性检查当前模型的 WSS 值。
下图对比了不同聚类结果下的 WSS 值:

在之前的模型建立中,通过绘制散点图来观察数据大致可以被聚合成的类别数量。但在没有提前指定数据类别数量的情况下,如果数据维度很高或者数据量过大,那么就无法以直观的形式检查它可能的类别数量。
有些时候即便以可视化的形式展现出来,也未必能很好地判断聚合类别数。例如,考虑以下数据点集合在不同聚类数下的结果:

检查结果可以发现,当聚合成 2 、3 、4 类时的结果似乎都有一定道理。
可以使用 WSS 来判断最好的结果,但是随着聚类个数的增加,聚类中心也变多了,各个点到聚类中心的距离肯定更近。如果将不同聚类数以及对应的最好的 WSS 值绘制在图表上,会得到以下折线:
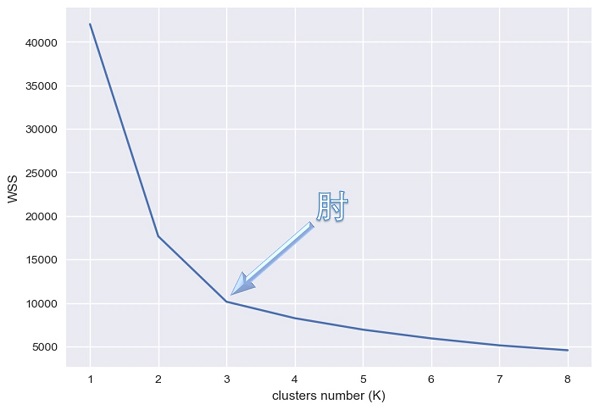
在折线上通常会出现一个拐点,这个拐点称为“肘”(elbow)。在肘部对应的 K 值之前,每增加一个分类数可以使 WSS 快速下降;但在肘部之后,更多的分类数对 WSS 的影响并不明显。在不清楚合适分类数的情况下,肘部对应的 K 值是一个不错的选择。
如果将折线的两端连成一条直线,那么肘部在 \\( y \\) 方向上离这条直线的距离一般最远。因此,可以使用以下代码计算肘部对应的 K 值:
这种方式比较简单,但结果比较粗糙。一种更精确但也更复杂的方法是使用轮廓系数(silhouette value)。样本点轮廓系数的计算公式为:
其中 \\( a(i) \\) 是样本 \\( i \\) 与同一集群中其它样本的平均距离,\\( b(i) \\) 是平均最近集群距离(即到不包括自身集群的最近集群实例的平均距离)。轮廓系数的取值范围是 \\( [-1, +1] \\) ,该值越接近 +1 ,表示对应的样本点越好地位于自身的集群中,并且远离其它集群;接近 0 的轮廓系数表示它接近一个集群的边界;接近 -1 的系数意味着样本点可能分配给了错误的集群。
可以使用以下代码计算轮廓分数(所有实例的平均轮廓系数):
将不同聚类数的轮廓分数以折线图的形式绘制出来,结果为:
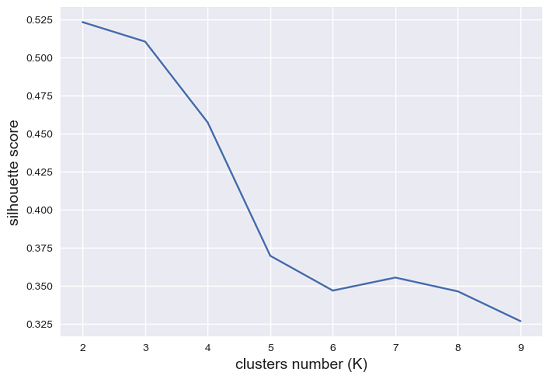
从结果中可以看到,虽然使用肘点判断结果为 \\( k=3 \\) 时效果最好,但轮廓系数判断该值使得一个集群可能会被不合理地拆分,使得许多样本点落在了它们的分界线上,说明 \\( k=2 \\) 可能是一个更好的集群数。
Scikit-Learn 还提供了 KMeans 算法的一个变种,它在每次迭代中采用随机抽样的方法选择小批量的数据子集,在减小计算时间的同时能够尽可能的拟合原始的数据。这在数据集过大时可以显著提升算法的速度,并且可以处理内存无法容纳的超大数据集。可以使用 MiniBatchKMeans 类调用该算法,使用方式和 KMeans 类是一致的:
KMeans 是一种经典的聚类算法,它适用于任意维度数据的聚类,但在聚类时需要提前知道或判断 K 值。KMeans 的聚类依据是更接近的集群中心点,这使得在实际聚类时每个集群边界总是线性的。使用 Voronoi 图可以很清晰地表现这一原理,图中落在由中心点确定的多边形内的样本会被归为该类:
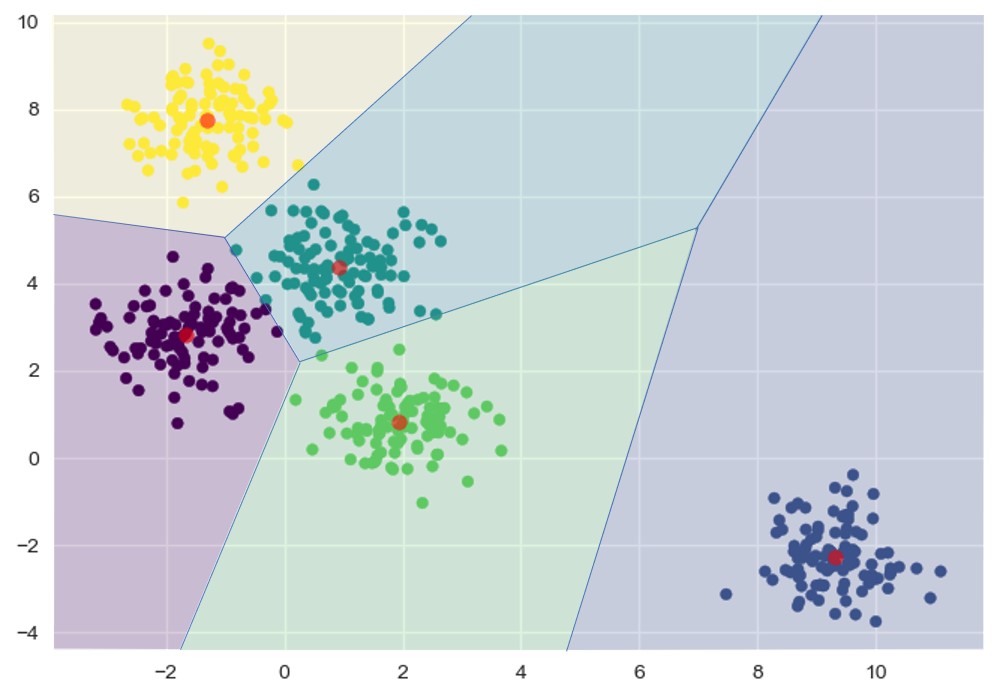
由于只能确定线性聚类边界,当集群呈现非线性的复杂形状时,KMeans 往往会不起作用,例如以下数据:
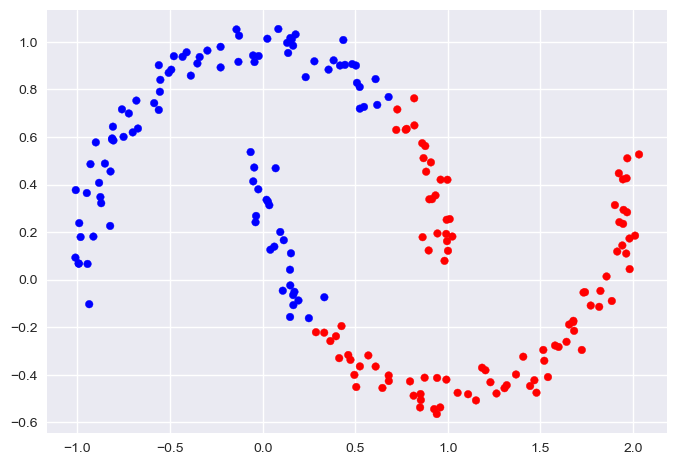
这时候就不能使用 KMeans 了。不过有一种算法可以很好地处理这种形式的聚类问题:DBSCAN。
DBSCAN算法
算法原理
DBSCAN 算法全称 Density-Based Spatial Clustering of Applications with Noise ,是一种以密度为基础的空间聚类算法,可以用密度的形式发现任意形状的集群。该算法将集群定义为具有足够密度的连续区域,因此可以处理任意形状的边界,如下图所示:

DBSCAN 算法的基本步骤为:先随机选取一个点,以该样本点为圆心,按照设定的半径作圆。如果圆内的样本数大于等于设定的阈值(密度),则将这些样本归为一类。接着选定圆内的其它样本点,继续作圆;如果某个圆内的样本数小于阈值,则放弃该圆的绘制。不断重复以上步骤直到没有可画的圆为止,并将这些圆内的样本点归为一个集群。
下图展示了该算法的原理:
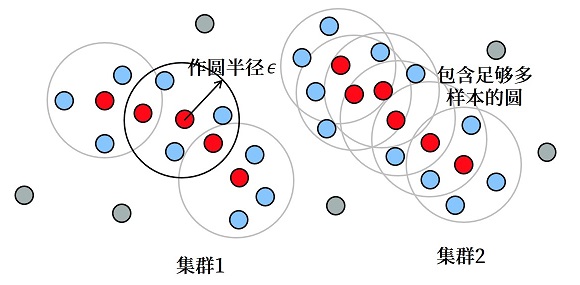
注意,以上两图内都存在不属于高密度集群内的点(游离点),因此这也是 DBSCAN 算法的优势之一,即可以使用密度的概念剔除不属于任一类别的噪点。
代码实现
DBSCAN 算法的实现与 KMeans 算法遵循同样的接口。它可以调整的参数有 eps(作圆的半径)和 min_samples(圆内的最少样本数),以此来控制密度:
聚类的结果也可以通过 .labels_ 属性检查。之前说过 DBSCAN 算法可以判断噪点的存在,噪点在 .labels_ 结果内对应的标签均为 -1 ,因此可以用类型以下的形式在散点图中标出噪点,效果与上文展示的图片类似:
DBSCAN 的结果还包含了 .components_ 属性,可以得到半径内包含足够样本的核心实例本身,或者可以使用 .core_sample_indices_ 属性获取它们的索引。
虽然 DBSCAN 的接口遵循 Scikit-Learn 接口的标准,但它没有 .predict() 方法。这是由于聚类算法不一定适合用于分类:有时候预测一个新样本分类的难度可能和重新聚类差别不大,尤其是 DBSCAN 可能出现同时被划分到两个类别且难以判断哪个是更好的情况。因此聚类完成后可以将结果应用到其余的分类器中,例如 KMeans 算法的思路就和 \\( K=1 \\) 的 K 近邻算法很像。
结果分析
和 KMeans 一样,DBSCAN 的参数 eps 和 min_samples 也并不好直接确定。若密度选取过小,两个邻近集群可能被合并;若密度选择过大,则一个集群可能会被拆分。
参数 min_samples 可以使用以下的原则确定:
eps 的值可以使用绘制 K-距离曲线的方式得到。K-距离表示每个样本第 K 个最近邻样本距离。将数据集所有点对应的 K 近邻距离按照降序方式排序,便可以绘制出 K 距离图线。
可以通过以下方式得到所有样本点排序后的 K-距离:
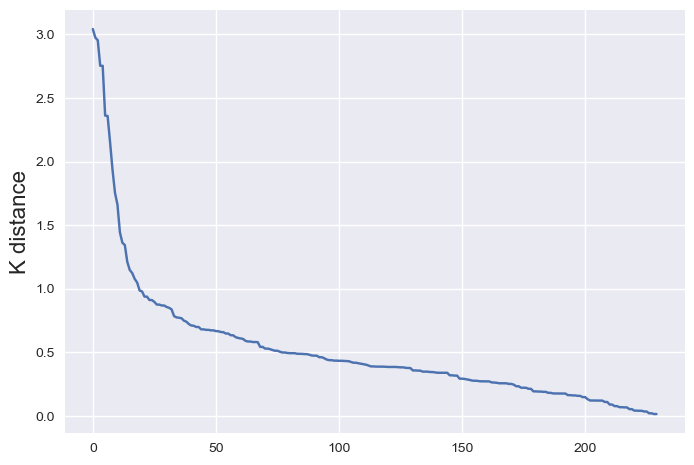
曲线图明显拐点位置为对应较好的参数。在本示例中,eps 可以取 1.0 左右。
最后要注意的是,虽然这种方式比起随机选择的参数具有一定的合理性,但是得到的参数仍然未必是合理的。
下图对比了 KMeans 算法与 DBSCAN 算法对同一批数据的聚类结果。对比结果可以发现:DBSCAN 算法在聚类时可以发现任意形状的簇将其聚为一类,而 KMeans 算法只是机械地将距离近的数据归到同一组:
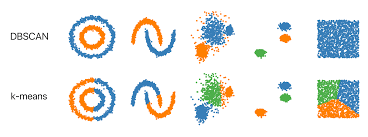
总的来说,DBSCAN 算法不需要事先知道集群数,并且可以发现任意形状的集群,初始中心点选择也不影响聚类结果。但它的特点决定了不适用于密度变化较大的数据,参数也难以确实最优值。因此如果难以通过可视化等方式检查数据并确定合适的参数的话,尽量还是谨慎选用该算法。
示例:图像颜色聚合
接下来通过一个具体的示例介绍聚类算法的使用。这里通过聚类算法分析一张图片的主要颜色组成,将其提取出来并用于压缩图像颜色。
一个图像由若干像素点组成,一般在网络上传输的图像每一个像素点都使用 RGB 色值表示,每一个色值占据一个字节。那么这样的一个图像可以使用形状为 (image_height, image_width, 3) 的数组描述。可以使用以下代码获取这样的数值:
考虑到这里只关注像素的 RGB 通道,对像素的位置不感兴趣,因此可以将其转为自变量为 RGB 值的二维数据:
然后利用以上数据建立聚类模型。由于自变量的密度不好确定且可能改变,并且为了便于使用中心值描述每一类的结果,在已知 K 值的情况下,使用 KMeans 是一个更好的选择:
以下展示了部分示例图片聚合得到的主要颜色值:

可以根据结果,将一批图像通过二次聚类的方式按颜色分类,还可以用于将图像包含的颜色压缩。颜色压缩也很简单,只需要将每一类颜色都填充其中心点的色值即可:
以下对比了同一图像在不同颜色数下图像压缩的结果:
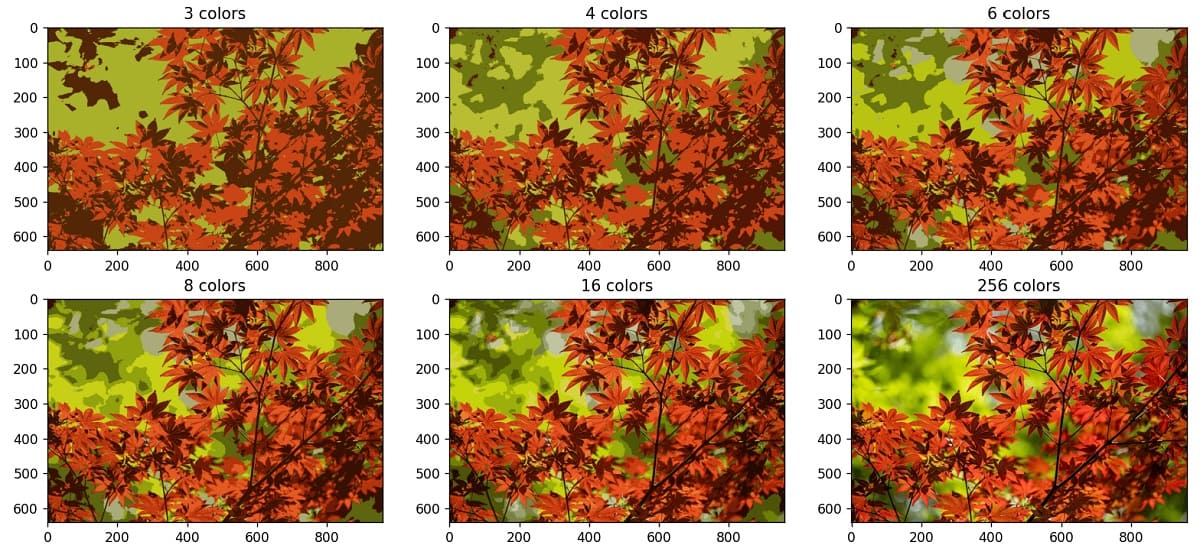



近期评论